A Study on Plithogenic Product Fuzzy Graphs with Application in Social network

T Bharathi; S Leo

doi:10.17485/IJST/v14i40.1298

Article

A Study on Plithogenic Product Fuzzy Graphs with Application in Social network

VIEWS 1766
PDF 326

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v14i40.1298

Year: 2021, Volume: 14, Issue: 40, Pages: 3051-3063

Original Article

A Study on Plithogenic Product Fuzzy Graphs with Application in Social network

T Bharathi¹, S Leo^2*

¹Assistant Professor, Department of Mathematics, Loyola College, University of Madras, Chennai, 600 034, Tamil Nadu, India
²Research Scholar, Department of Mathematics, Loyola College, University of Madras, Chennai, 600 034, Tamil Nadu, India

*Corresponding Author
Email: [email protected]

Received Date:12 July 2021, Accepted Date:23 October 2021, Published Date:29 November 2021

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

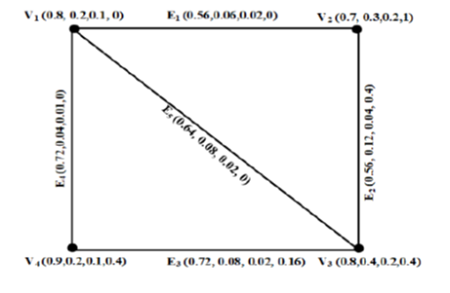
Objectives: The main objective of this study is to define Plithogenic product fuzzy graphs (PPFGs), and introduce its properties. Method: PPFGs is newly introduced as a new graphical model where P-vertices are characterized by four or more attributes and the attribute values of P-edges are computed using the product operator. Findings: Theoretical discussions and results related to PPFGs, and subgraphs, paths, cycles, trees, bridge and cut vertex in PPFGs are demonstrated with examples. A social network model based on the notion of PPFGs has been presented and analyzed to show the utility and the advantage of Plithogenic product fuzzy graph model. Novelty: Strong and weak P-vertices, and highly strong, strong and weak P-edges are identified to analyze the strength of connectivity between different units. P-order, P-size, P-vertex range, P-edge range, degree, total degree, and average P-weight of P-vertices are computed to examine proximity, significance and centrality of units.

Keywords: Plithogenic fuzzy sets; Fuzzy graphs; Plithogenic fuzzy graphs; Plithogenic product fuzzy graphs; Social networks

References

Zadeh LA. Fuzzy sets. Information and Control. 1965;8(3):338–353. Available from: https://dx.doi.org/10.1016/s0019-9958(65)90241-x
Mythili V, Kaliyappan M, Hariharan S. A Review of Fuzzy Graph Theory. International Journal of Pure and Applied Mathematics. 2017;113(12):187–195. Available from: https://acadpubl.eu/jsi/2017-113-pp/articles/12/21.pdf
Rosenfeld A. Fuzzy Graphs. In: Fuzzy Sets and their Applications to Cognitive and Decision Processes. (pp. 77-95) Academic Press. 1975.
Atanassov KT. Intuitionistic Fuzzy Sets. In: Fuzzy Sets and Systems. (pp. 87-96) 1986.
Parvathi R, Karunambigai MG. Intuitionistic Fuzzy Graphs. In: Computational Intelligence, Theory and Applications. (pp. 139-150) Springer Berlin Heidelberg. 2006.
Zuo C, Pal A, Dey A. New Concepts of Picture Fuzzy Graphs with Application. Mathematics. 2019;7(5):470. Available from: https://dx.doi.org/10.3390/math7050470
Shi X, Kosari S. Certain Properties of Domination in Product Vague Graphs With an Application in Medicine. Frontiers in Physics. 2021;9:385. Available from: https://dx.doi.org/10.3389/fphy.2021.680634
Rosyida I, Suryono S. Coloring picture fuzzy graphs through their cuts and its computation. International Journal of Advances in Intelligent Informatics. 2021;7(1):63–75. Available from: https://dx.doi.org/10.26555/ijain.v7i1.612
Bhattacharya A, Pal M. Fuzzy covering problem of fuzzy graphs and its application to investigate the Indian economy in new normal. Journal of Applied Mathematics and Computing. 2021;p. 1–32. Available from: https://dx.doi.org/10.1007/s12190-021-01539-4
Smarandache F. Neutrosophic set - a generalization of the intuitionistic fuzzy set. IEEE. p. 38–42.
Vasantha WB, Ilanthenral K, Smarandache K, F. Neutrosophic Graphs : A New Dimention to Graph Theory Brussels: EuropaNova. 2015.
Smarandache F. Refined literal indeterminacy and the multiplication law of sub-indeterminacies. Infinite Study. 2015. Available from: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.962.626&rep=rep1&type=pdf#page=60
Broumi S, Talea M, Bakali A, Smarandache F. Single Valued Neutrosophic Graphs. Journal of New Theory. 2016;(10) 86–101. Available from: https://dergipark.org.tr/en/download/article-file/407546
Smarandache F. Plithogeny, Plithogenic Set, Logic, Probability, and Statistics Brussels, Belgium. Pons Editions. 2017.
Vasantha WB, Ilanthenral K, Smarandache F. Plithogenic Graphs Bruxelles. (Vol. EuropaNova: 2020).
Yeh RT, Bang SY. Fuzzy relations, fuzzy graphs, and their applications to clustering analysis. In: Fuzzy sets and their applications to Cognitive and Decision Processes . (pp. 125-149) Academic Press. 1975.
Gani AN, Ahamed MB. Order and size in fuzzy graphs. Bulletin of Pure and Applied Sciences. 2003;22(1):145–148.
Rashmanlou H, Samanta S, Pal M, Borzooei RA. Product of bipolar fuzzy graphs and their degree. International Journal of General Systems. 2016;45(1):1–14. Available from: https://dx.doi.org/10.1080/03081079.2015.1072521
Pal A, Samanta S, Pal M. Concept of fuzzy planar graphs. In: Science and Information Conference. IEEE. p. 557–563.
Samanta S, Pal M. Fuzzy k-Competition Graphs and p-Competition Fuzzy Graphs. Fuzzy Information and Engineering. 2013;5(2):191–204. Available from: https://dx.doi.org/10.1007/s12543-013-0140-6
Samanta S, Pal M. Fuzzy Planar Graphs. IEEE Transactions on Fuzzy Systems. 2015;23(6):1936–1942. Available from: https://dx.doi.org/10.1109/tfuzz.2014.2387875
Al-Hawary T, Horani B. On Product Fuzzy Graphs. Annals of Fuzzy Mathematics and Informatics. 2016;12(2):279–294.
Samanta S, Pal M. A new approach to social networks based on fuzzy graphs. Turkish Journal of Fuzzy Systems. 2014;5(2):78–99.
Casasús-Estellés T, Yager RR. Fuzzy Concepts in Small Worlds and the Identification of Leaders in Social Networks. Information Processing and Management of Uncertainty in Knowledge-Based Systems. 2014;p. 37–45.
Binu M, Mathew S, Mordeson JN. Connectivity status of fuzzy graphs. Information Sciences. 2021;573:382–395. Available from: https://dx.doi.org/10.1016/j.ins.2021.05.068
Naeem T, Gumaei A, Jamil MK, Alsanad A, Ullah K. Connectivity Indices of Intuitionistic Fuzzy Graphs and Their Applications in Internet Routing and Transport Network Flow. Mathematical Problems in Engineering. 2021;2021:1–16. Available from: https://dx.doi.org/10.1155/2021/4156879
Mahapatra R, Samanta S, Pal M, Xin Q. Link Prediction in Social Networks by Neutrosophic Graph. International Journal of Computational Intelligence Systems. 2020;13(1):1699–1713. Available from: https://dx.doi.org/10.2991/ijcis.d.201015.002
Khan WA, Ali B, Taouti A. Bipolar Picture Fuzzy Graphs with Application. Symmetry. 2021;13(8 (1427)):1–22. Available from: https://dx.doi.org/10.3390/sym13081427
Sunita MS, Mathew S. Fuzzy Graph Theory: A survey. Annals of Pure and Applied Mathematics. 2013;4(1):92–110.

Copyright

© 2021 Bharathi & Leo. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)