• P-ISSN 0974-6846 E-ISSN 0974-5645

Indian Journal of Science and Technology

Article

Beta Lehmann-2 power function distribution with application to bladder cancer susceptibility and failure times of air-conditioned system
  • VIEWS 1417
  • PDF 269

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v13i23.178

Year: 2020, Volume: 13, Issue: 23, Pages: 2371-2386

Original Article

Beta Lehmann-2 power function distribution with application to bladder cancer susceptibility and failure times of air-conditioned system

Azam Zaka1*, Ahmad Saeed Akhter2, Riffat Jabeen3

1Government College of Science, Wahdat Road, Lahore, Pakistan. Tel.: +93-300-4364368
2College of Statistical and Actuarial Sciences, University of the Punjab, Lahore, Pakistan
3COMSATS University Islamabad Lahore Campus, Lahore, Pakistan

*Corresponding author
Azam Zaka
Tel.: +93-300-4364368
Email: [email protected]

 

Received Date:07 April 2020, Accepted Date:19 May 2020, Published Date:07 July 2020

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

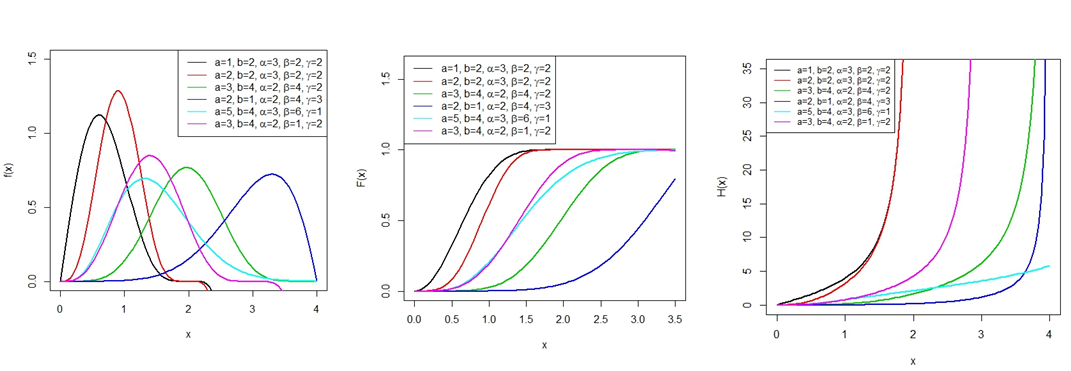
Objectives: Probability distributions have great use in reliability engineering where the researchers try to find the distribution of the different processes. To meet the needs of the reliability engineers, we have proposed a simple probability distribution named as Beta Lehman-2 which may be proved more useful as compared to already existing models of the probability distributions. The aim of the study is to show the performance of the proposed distribution over already existing distributions. Methods: In this study, a new Beta Lehmann-2 Power function distribution (BL2PFD) is proposed. We suggest a new generator that will modify the Power function distribution called Beta Lehmann-2 generator (BL2-G). Findings: The various properties of the new distribution have been discussed in detail such as moments, vitality function, conditional moments and order statistics etc. We have also characterized the BL2PFD based on conditional variance. This distribution can be used for approximately symmetric data (normal data), positive and negative skewed data. Application: The application of this distribution is illustrated by using data sets from medical and engineering sources. The shape of the new distribution has been studied for applied sciences. After analyzing data, we conclude that the proposed model BL2PFD perform better in all the data sets while compared to different competitor models.

Keywords: Beta Lehmann-2 Power function distribution; Characterization of truncated distribution; Lehmann alternatives; Percentile estimator; Power function distribution

References

  1. Dallas AC. Characterization of Pareto and power function distribution. Annals of the Institute of Statistical Mathematics. 1976;28:491–497.
  3. Ahsanullah M, Shakil M, Kibria B. A characterization of the power function distribution based on lower records. Prob Stat Forum. 2013;6:68–72.
  4. Chang SK. Characterizations of the power function distribution by the independence of record values. Journal of the Chungcheong Mathematical Society. 2007;20:139–146.
  5. Dorp JRv, Kotz S. The Standard Two-Sided Power Distribution and its Properties. The American Statistician. 2002;56(2):90–99. Available from: https://dx.doi.org/10.1198/000313002317572745
  6. Saleem M, Aslam M, Economou P. On the Bayesian analysis of the mixture of power function distribution using the complete and the censored sample. Journal of Applied Statistics. 2010;37(1):25–40. Available from: https://dx.doi.org/10.1080/02664760902914557
  7. Zaka A, Akhter AS. METHODS FOR ESTIMATING THE PARAMETERS OF THE POWER FUNCTION DISTRIBUTION. Pakistan Journal of Statistics and Operation Research. 2013;9(2):213. Available from: https://dx.doi.org/10.18187/pjsor.v9i2.488
  8. Tahir MH, Alizadeh M, Mansoor M, Cordeiro GM, Zubair M. THE WEIBULL-POWER FUNCTION DISTRIBUTION WITH APPLICATIONS. Hacettepe Journal of Mathematics and Statistics. 2014;45(42):1. Available from: https://dx.doi.org/10.15672/hjms.2014428212
  9. Hanif S, Al-Ghamdi SD, Khan K, Shahbaz MQ. 2015. Available from: https://www.researchgate.net/publication/294428604
  10. Shahzad MN, Asghar Z. Transmuted Power Function Distribution : A more flexible Distribution. Journal of Statistics and Management Systems. 2016;19(4):519–539. Available from: https://dx.doi.org/10.1080/09720510.2015.1048096
  11. Shaw WT, Buckley IR. 2009.
  12. Okorie IE, Akpanta AC, Ohakwe J, Chikezie DC. The modified Power function distribution. Cogent Mathematics. 2017;4(1). Available from: https://dx.doi.org/10.1080/23311835.2017.1319592
  14. Haq MA, Usman RM, Bursa N, Ozel G. McDonald Power function distribution with theory and applications. International Journal of Statistics and Economics. 2018;19(2):89–107.
  15. Ibrahim M. The Kumaraswamy Power function distribution. Journal of Statistics Applications and Probability. 2017;6(1).
  16. Jabeen R, Zaka A. Estimation of parameters of the continuous uniform distribution: Different classical methods. Journal of Statistics and Management Systems. 2019;p. 1–19. Available from: https://dx.doi.org/10.1080/09720510.2019.1639948
  17. Zaka A, Akhter AS, Jabeen R. THE EXPONENTIATED GENERALIZED POWER FUNCTION DISTRIBUTION: THEORY AND REAL LIFE APPLICATIONS. Advances and Applications in Statistics. 2020;61(1):33–63. Available from: https://dx.doi.org/10.17654/as061010033
  18. Lehman EL. The power of rank tests. Annals of Mathematical Statistics. 1953;24:28–43.
  19. Eugene N, Lee C, Famoye F. BETA-NORMAL DISTRIBUTION AND ITS APPLICATIONS. Communications in Statistics - Theory and Methods. 2002;31(4):497–512. Available from: https://dx.doi.org/10.1081/sta-120003130
  20. Glaser R. Bathtub and Related Failure Rate Characterizations. Journal of the American Statistical Association. 1980;75:667–672.
  21. Dubey SD. Some Percentile Estimators for Weibull Parameters. Technometrics. 1967;9(1):119–129. Available from: https://dx.doi.org/10.1080/00401706.1967.10490445
  22. Marks NB. Estimation of Weibull parameters from common percentiles. Journal of Applied Statistics. 2005;32(1):17–24. Available from: https://dx.doi.org/10.1080/0266476042000305122
  23. Zea LM, Silva RB, Bourguignon M, Santos AM, Cordeiro GM. The Beta Exponentiated Pareto Distribution with Application to Bladder Cancer Susceptibility. International Journal of Statistics and Probability. 2012;1(2):8–19. Available from: https://dx.doi.org/10.5539/ijsp.v1n2p8
  24. Lee ET, Wang JW. Statistical Methods for Survival Data Analysis. New York. Wiley. 2003.
  25. Haq MAU, Hamedani GG, Elgarhy M, Ramos PL. Marshall-Olkin Power Lomax Distribution: Properties and Estimation Based on Complete and Censored Samples. International Journal of Statistics and Probability. 2019;9(1):48. Available from: https://dx.doi.org/10.5539/ijsp.v9n1p48
  26. Aarset MV. How to Identify a Bathtub Hazard Rate. IEEE Transactions on Reliability. 1987;R-36(1):106–108. Available from: https://dx.doi.org/10.1109/tr.1987.5222310
  27. Dey S, Alzaatreh A, Zhang C, Kumar D. A New Extension of Generalized Exponential Distribution with Application to Ozone Data. Ozone: Science & Engineering. 2017;39:273–285. Available from: https://dx.doi.org/10.1080/01919512.2017.1308817
  28. Haq MAu, Usman RM, Hashmi S, Al-Omeri AI. The Marshall-Olkin length-biased exponential distribution and its applications. Journal of King Saud University - Science. 2019;31(2):246–251. Available from: https://dx.doi.org/10.1016/j.jksus.2017.09.006
  29. Ramadan DA, Magdy W. On the alpha-power inverse Weibull distribution. International Journal of Computer Applications. 2018;181(11):6–12.
  30. Ihtisham S, Khalil A, Manzoor S, Khan SA, Ali A. Alpha-Power Pareto distribution: Its properties and applications. PLOS ONE. 2019;14(6):e0218027. Available from: https://dx.doi.org/10.1371/journal.pone.0218027
  31. ZeinEldin RA, Haq MAu, Hashmi S, Elsehety M. Alpha Power Transformed Inverse Lomax Distribution with Different Methods of Estimation and Applications. Complexity. 2020;2020:1–15. Available from: https://dx.doi.org/10.1155/2020/1860813

Copyright

© 2020 Zaka, Akhter, Jabeen. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. 
Published By Indian Society for Education and Environment (iSee)

  • 08 July 2020

Year: 2020, Volume: 13, Issue: 23

Article Metrics


Post Graduate Fellowship in Research Communication

More articles

DON'T MISS OUT!

Subscribe now for latest articles and news.