Mathematical Modeling and its Stability Analysis of an SEIR Model to Control Dengue by Segregating the Infective: An Approach for Efficient Resource Allocation

A Joshua Cyril Yagan; D Jasmine

doi:10.17485/IJST/v17i17.247

Article

Mathematical Modeling and its Stability Analysis of an SEIR Model to Control Dengue by Segregating the Infective: An Approach for Efficient Resource Allocation

VIEWS 60
PDF 29

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v17i17.247

Year: 2024, Volume: 17, Issue: 17, Pages: 1800-1812

Original Article

Mathematical Modeling and its Stability Analysis of an SEIR Model to Control Dengue by Segregating the Infective: An Approach for Efficient Resource Allocation

A Joshua Cyril Yagan^1*, D Jasmine¹

¹Department of Mathematics, Bishop Heber College (Autonomous), Affiliated to Bharathidasan University, Tiruchirappalli, 620 017, Tamil Nadu, India

*Corresponding Author
Email: [email protected]

Received Date:30 January 2024, Accepted Date:10 April 2024, Published Date:24 April 2024

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

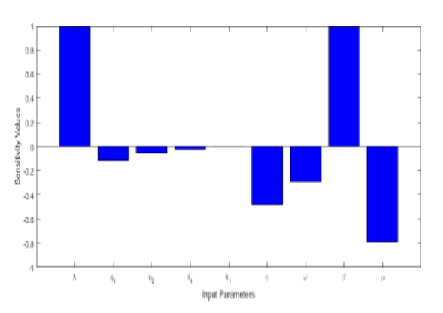
Objectives: Many research deals study on modeling the spread of dengue virus disease. The study dealing mathematical model to influence the concept of segregating infective is very important as it makes an organised practice of treatment which enlightens civilization. This article focuses on the same and frames a model with a proper analysis. Methods: BhirkoffRhota theorem helps in proving the boundedness of the model. By using the Next-Generation matrix the expression for Reproduction number is determined. The Routh-Hurwitz stability criterion is used to reveal the Local Stability of the proposed model. The aid of Lyapunov-LaSalle's principle proves the Global Stability. Findings: The proposed model is found to be positive and also bounded. Moreover, the equilibrium points exists and stable locally and globally. The numerical simulation shows that at the disease-free equilibrium and at the endemic equilibrium proving the stability of the model numerically. The comparative analysis of the model results in revealing the fact that the proposed model controls the infective better than the usual model. Novelty: The article differs from the usual model by incorporating the idea of categorizing the infected population into 3 phase namely febrile, critical and convalescent concluding that the use of proposed model helps in effective treatment and in efficient management of hospital resources in a systematic way.

Keywords: Epidemic, Treatment Class, SEIR model, Jacobian matrix, Sensitivity index

References

Dengue cases January-December 2023. European Centre for Disease Prevention and Control. Available from: https://www.ecdc.europa.eu/en/publications-data/dengue-cases-january-december-2023
Abidemi A, Fatmawati, Peter OJ. An optimal control model for dengue dynamics with asymptomatic, isolation, and vigilant compartments. Decision Analytics Journal. 2024;10:1–20. Available from: https://dx.doi.org/10.1016/j.dajour.2024.100413
Khan MA, Fatmawati. Dengue infection modeling and its optimal control analysis in East Java, Indonesia. Heliyon. 2021;7(1):1–13. Available from: https://dx.doi.org/10.1016/j.heliyon.2021.e06023
Aguiar M, Anam V, Blyuss KB, Estadilla CDS, Guerrero BV, Knopoff D, et al. Mathematical models for dengue fever epidemiology: A 10-year systematic review. Physics of Life Reviews. 2022;40:65–92. Available from: https://dx.doi.org/10.1016/j.plrev.2022.02.001
Alshehry AS, Yasmin H, Khammash AA, Shah R. Numerical analysis of dengue transmission model using Caputo–Fabrizio fractional derivative. Open Physics. 2024;22(1):1–19. Available from: https://dx.doi.org/10.1515/phys-2023-0169
Colston JM. Elucidating the Impacts of Climate on Dengue Transmission Through Mathematical Models: New Evidence From a Recent Outbreak on the Island of Réunion. The Journal of Infectious Diseases. 2024;229(1):1–3. Available from: https://dx.doi.org/10.1093/infdis/jiad473
Olarte JA, Muñoz A. Modeling the dengue fever transmission in a periodic environment. Revista Colombiana de Matemáticas. 2021;55(1):71–107. Available from: https://dx.doi.org/10.15446/recolma.v55n1.99099
Rahman MS, Mehejabin F, Rahman MA, Rashid R. A case-control study to determine the risk factors of dengue fever in Chattogram, Bangladesh. Public Health in Practice. 2022;4:1–6. Available from: https://dx.doi.org/10.1016/j.puhip.2022.100288
Diabaté AB, Sangaré B, Koutou O. Mathematical modeling of the dynamics of vector-borne diseases transmitted by mosquitoes : taking into account aquatic stages and gonotrophic cycle. Nonautonomous Dynamical Systems. 2022;9(1):205–236. Available from: https://dx.doi.org/10.1515/msds-2022-0155
Islam N, Borhan JRM, Prodhan R. Application of Mathematical Modeling: A Mathematical Model for Dengue Disease in Bangladesh. International Journal of Mathematical Sciences and Computing. 2024;10(1):19–30. Available from: https://dx.doi.org/10.5815/ijmsc.2024.01.03
Li-Martín A, Reyes-Carreto R, Vargas-De-León C. Dynamics of a dengue disease transmission model with two-stage structure in the human population. Mathematical Biosciences and Engineering. 2022;20(1):955–974. Available from: https://dx.doi.org/10.3934/mbe.2023044
Lamis A, Tasman H. Dynamic analysis of a coinfection model of dengue and asymptomatic and symptomatic COVID-19. ITM Web of Conferences. 2024;61:1–15. Available from: https://dx.doi.org/10.1051/itmconf/20246101007
Bhuju G, Phaijoo GR, Gurung DB. Fuzzy Approach Analyzing SEIR-SEI Dengue Dynamics. BioMed Research International. 2020;2020:1–11. Available from: https://dx.doi.org/10.1155/2020/1508613
Sa'adah A, Sari DK. Mathematical Models of Dengue Transmission Dynamics with Vaccination and Wolbachia Parameters And Seasonal Aspects. BAREKENG: Jurnal Ilmu Matematika dan Terapan. 2023;17(4):2305–2316. Available from: https://dx.doi.org/10.30598/barekengvol17iss4pp2305-2316
Chamnan A, Pongsumpun P, Tang IM, Wongvanich N. Optimal Control of Dengue Transmission with Vaccination. Mathematics. 2021;9(15):1–33. Available from: https://dx.doi.org/10.3390/math9151833
Khan A, Zarin R, Hussain G, Ahmad NA, Mohd MH, Yusuf A. Stability analysis and optimal control of covid-19 with convex incidence rate in Khyber Pakhtunkhawa (Pakistan) Results in Physics. 2021;20:1–17. Available from: https://dx.doi.org/10.1016/j.rinp.2020.103703
Xu Z, Zhang H, Yang D, Wei D, Demongeot J, Zeng Q. The Mathematical Modeling of the Host–Virus Interaction in Dengue Virus Infection: A Quantitative Study. Viruses. 2024;16(2):1–17. Available from: https://dx.doi.org/10.3390/v16020216
Yagan AJC, Jasmine D. Significance of an SEIHR Model with Preventive Class in Declining the Spread of COVID-19. Indian Journal Of Science And Technology. 2023;16(Special Issue 3):14–21. Available from: https://dx.doi.org/10.17485/ijst/v16isp3.icrtam130
Obasi C, Mbah GCE. On the stability analysis of a mathematical model of Lassa fever disease dynamics. International Journal of Mathematical Analysis and Modelling. 2019;2(1):135–144. Available from: https://tnsmb.org/journal/index.php/ijmam/article/view/16
Delamater PL, Street EJ, Leslie TF, Yang YT, Jacobsen KH. Complexity of the Basic Reproduction Number (R0) Emerging Infectious Diseases. 2019;25(1):1–4. Available from: https://dx.doi.org/10.3201/eid2501.171901
Trawicki MB. Deterministic Seirs Epidemic Model for Modeling Vital Dynamics, Vaccinations, and Temporary Immunity. Mathematics. 2017;5(1):1–19. Available from: https://dx.doi.org/10.3390/math5010007
India -2024. macrotrends. Available from: https://www.macrotrends.net/countries/IND/india/lifeexpectancy#: :text=The%20life%20expectancy%20for%20India, a%200.33%25%20incr ease%20from %202020
Almeida R. Analysis of a fractional SEIR model with treatment. Applied Mathematics Letters. 2018;84:56–62. Available from: https://doi.org/10.1016/j.aml.2018.04.015
Rodrigues HS, Monteiro MTT, Torres DFM. Sensitivity Analysis in a Dengue Epidemiological Model. Conference Papers in Science. 2013;2013:1–7. Available from: https://dx.doi.org/10.1155/2013/721406

Copyright

© 2024 Yagan & Jasmine. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)