Indian Journal of Science and Technology

Abstract

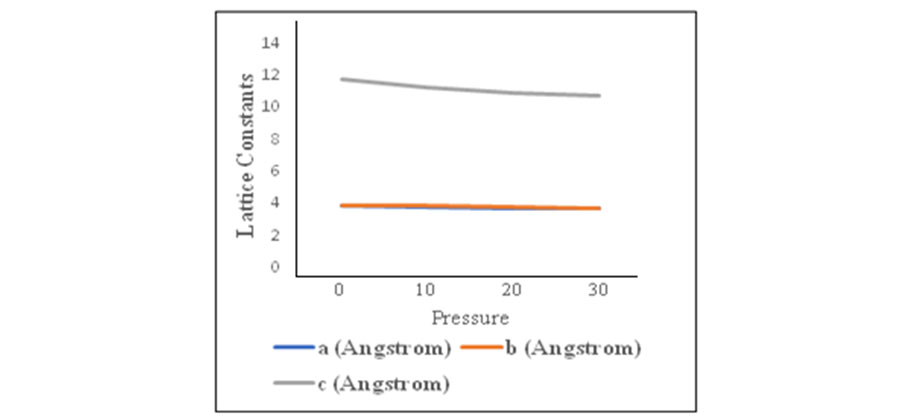
Background/Objectives: The crystal structure of YBCO Superconductor has fascinated the material science research group. The calculation of mechanical properties of YBCO Superconductor under pressure is the main focus in this research work. Methods/Statistical analysis: Density Functional Theory calculations using Quantum ESPRESSO under high pressure increasing systematically have been calculated and performed for YBa2Cu3o7 Superconductor. The only input required is the lattice parameters at corresponding pressure of materials which are predicted using first principle computational methods at desired high-pressure state. Findings: The lattice constants, variations, volume, density, Bulk modulus (B), Young modulus (E), Shear modulus (S) and Poisson ratio (n)values are calculated under pressure up to 30 GPa for YBCO Superconductor. Voigt-Reuss-Hill Approximations, Debye Sound velocities(ϑD), Debye temperature(θD) and Pugh's ratio(B/G) values have been calculated under pressure for YBCO Superconductor in this research work. Novelty/Applications: A larger poisson's ratio value indicates ductile behavior and another criterion often used to differentiate between ductile and brittle behavior is the Poisson's ratio. Poisson's ratio greater than 0.26 implies the ductile behavior. With the application of elastic constants, we have obtained the Debye temperature and other physical quantities of YBa2Cu3o7 under pressure.

Keywords: YBCO superconductor; density functional theory (DFT); lattice constants; pressure; quantum ESPRESSO