Indian Journal of Science and Technology

Abstract

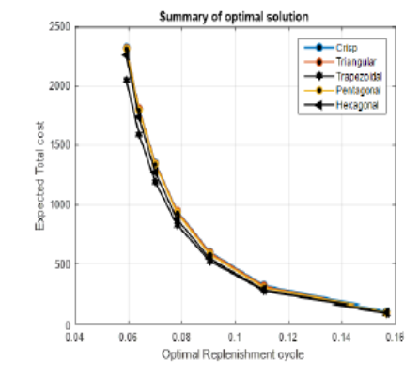
Objectives: To propose suitable inventory system with advance payment in a fuzzy situation by employing four types of fuzzy numbers that are triangular, trapezoidal, pentagonal and Hexagonal. Methods: We use the same numerical data as in Priyan et al.(1) to verify the results obtained by this research. To obtain the minimum total cost and the optimum solution, a comparison is made by employing four types of fuzzy numbers. Two inventory models are proposed here. Initially, crisp models are developed with fuzzy total inventory cost along crisp optimal replenishment cycle. Next, the fuzzy model is also formulated with fuzzy total inventory cost and fuzzy optimal replenishment cycle. Graded mean integration method is employed to defuzzify the total inventory cost and the extension of the Lagrangian method is used to determine the optimal replenishment cycle. Findings: Our results indicate that the optimal solutions of the fuzzy model slightly fluctuate from the solutions of the crisp model. Numerical examples have been given in order to show the applicability of the proposed model. We obtain minimum total cost when we defuzzify the trapezoidal fuzzy parameters using graded mean integration method. Novelty: In real-world circumstances, costs might be influenced by a foreign currency in which the expenses are frequently unknown. Instead of a stochastic environment, the decision-maker in this case is faced with a fuzzy one. This study is unique in itself as it undertakes to study inventory models with different fuzzy numbers. The research reveals that the fuzzy model, which has been defuzzified with the graded mean integration method, shows a proof of savings of 25% to 40% in the analytical solution compared to the previous model. Our model helps the decision maker to tackle the uncertainties in accounting flexibility in the input factors that always fit the real situation. Keywords: Inventory costs; Advance payment; Fuzzy numbers; Graded mean integration method; Lagrangian method