Indian Journal of Science and Technology

Abstract

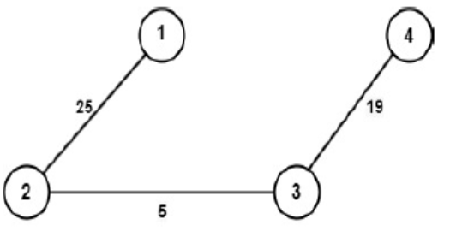
Objective: The symmetric encryption technique is one of the most important fields for securing communications between people. In order to produce complex ciphertext, we are introducing the new enciphering technique with the help of the Hamiltonian path, a self-invertible key matrix for encryption and decryption. Methods: There are many kinds of symmetric enciphering methods, like the Caesar Cipher, Atbash Cipher, Hill Cipher, etc. All these methods use a common key for encryption, and while decrypting the inverse of that matrix should be found, it is also too hard to share the common key. To reduce this terminology, we proposed the novel enciphering method with the help of a self-invertible key matrix. Findings: We are using the generated selfinvertible key matrix as a key matrix; the degree of the self-invertible matrix is even. If our graph does not form an even-degree adjacency matrix, then we have to make it into an even-degree adjacency matrix by adding dummy edges. Novelty: As we are using a self-invertible matrix as a key matrix, we do not need to compute the inverse of the key matrix for the process of decryption. This helps us to reduce the complexity of finding the inverse while decrypting the original message.

Keywords: Graph Theory Encryption; Hill Cipher; Hamiltonian Path; Adjacency Matrix; Self Invertible Matrix