Indian Journal of Science and Technology

Abstract

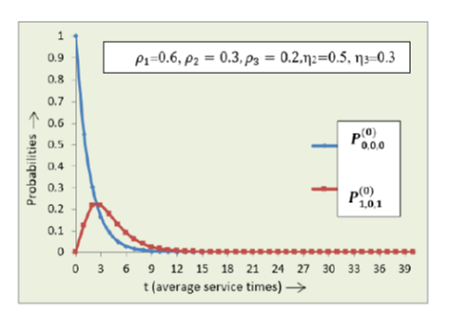
Objective: This study considered a system of retrial queues with two types of customers: high-priority and low-priority. This study deals to find the time dependent probabilities of exact number of arrivals and departures from the system when server is free or busy. Numerical solution and graphical representation will also be presented. Method: For this model, we solved difference differential equations recursively and used Laplace transformation to obtain the transient state probabilities of exact number of arrivals and departures from the system when server is free or busy. Findings: Timedependent probabilities of exact number of arrivals (primary arrivals, arrivals in high priority queue, arrivals in low priority queue) in the system and exact number of departures (primary departures, departures from high priority queue, departures from low priority queue) from the system by a given time for when the server is idle and when the server is busy are obtained. Various interesting performance measures along with some special cases are also obtained. Conversion of two state model into single state model was discussed. Numerical illustrations are also presented using MATLAB programming along with the busy period probabilities of the system and server. Novelty: In past research, models considered arrivals and departures from the orbit whereas in present model arrivals and departures from the system are studied along with the concept of retrial and priority customers. Applications: Priority retrial queues are used in many applications like real time systems, operating systems, manufacturing system, simulation and medical service systems.

Keywords: Arrivals; Departures; Probability; Priority; Retrial