Indian Journal of Science and Technology

Abstract

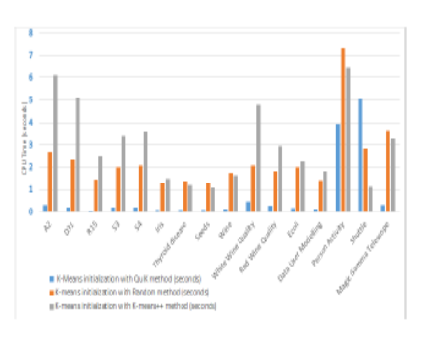
Objectives: This study aims to speed up the K-means algorithm by offering a deterministic quartile-based seeding strategy for initializing preliminary cluster centers for the K-means algorithm, enabling it to efficiently build high-quality clusters. Methods: We have investigated various cluster center initialization approaches in literature and presented our findings. For the Kmeans algorithm, we here propose a novel deterministic technique based on quartiles for finding initial cluster centers. To obtain the preliminary cluster centers, we have applied our suggested approach to the data set. The initial cluster centers determined by our suggested method are then entered into the K-means algorithm. The proposed seeding method is evaluated on sixteen benchmark clustering data sets: five synthetic and eleven real data sets. Python is used to run the simulation. Findings: Based on empirical results from experiments, it is evident that our proposed cluster center initialization method allows the K-means algorithm to form clusters with SSE values comparable to the minimum SSE values produced by repeated Random or Kmeans++ initializations. Furthermore, our deterministic initialization strategy assures that the K-means algorithm converges faster than the Random and K-means++ initialization techniques. Novelty: In this study, we explore the potential of quartile-based seeding as a technique of accelerating the Kmeans algorithm. Needless to add, as our seeding method is deterministic, the requirement to run K-means repeatedly with different stochastic initializations is completely eliminated. Also, our initialization strategy assures that there is remarkable saving in execution time as compared to the Random and Kmeans++ initialization techniques. Moreover, it is found that after initializing with our offered method, the solution obtained with just a single run of K-means produces optimal clusters. Applications: Our proposed seeding technique will be helpful for initializing the K-means algorithm in time-sensitive applications, applications managing large amounts of data, and applications looking for deterministic cluster solutions.

Keywords: Kmeans Algorithm; Initialization Method; Speeding Kmeans; Quartiles; Clustering; Deterministic Initialization Method