An Efficient Transform based Low Rank Tensor Completion to Extreme Visual Recovery

Sunil Kumar Jyothula; Jaya Chandra Prasad Talari

doi:10.17485/IJST/v15i14.264

Article

An Efficient Transform based Low Rank Tensor Completion to Extreme Visual Recovery

VIEWS 1029
PDF 185

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v15i14.264

Year: 2022, Volume: 15, Issue: 14, Pages: 608-618

Original Article

An Efficient Transform based Low Rank Tensor Completion to Extreme Visual Recovery

Sunil Kumar Jyothula¹,^2*, Jaya Chandra Prasad Talari³

¹Research scholar, Department of Electronics and Communication Engineering, JNTUA, Anantapur, Andhra Pradesh, India
²Assistant Professor, Department of Electronics and Communication Engineering, Malla Reddy Engineering College, Secunderabad, Telangana, India
³Professor, Department of Electronics and Communication Engineering, Rajeev Gandhi Memorial College of Engineering and Technology, Affiliated to JNTUA, Nandyal, Andhra Pradesh, India

*Corresponding Author
Email: [email protected]

Received Date:31 January 2022, Accepted Date:20 February 2022, Published Date:09 April 2022

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

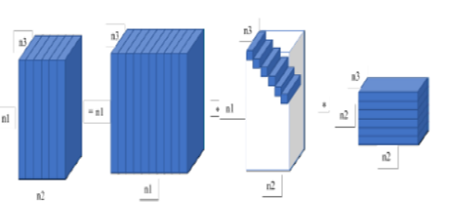
Objective: To propose an optimization approach in recovering of the corrupted tensors in the high dimensional real time data. Methods: The recovering of corrupted tensors is performed by low-rank tensor completion methods. The tensor decomposition methods are used in tensor completion methods. These Tensor decomposition methods; candecomp / parafac (CP), tucker and higher-order Singular Value Decomposition (HoSVD) are used to minimize the rank of a tensor data. The limitations are in finding the rank of a tensor. Findings: The recovered data using the lifting transform induced tensor- Singular Value Decomposition (t-SVD) technique were assessed utilizing the Peak Signal to Noise Ratio (PSNR), Structural Similarity (SSIM), Naturalness Image Quality Evaluator (NIQE), and Perceptual Image Quality Evaluator (PIQE). When compared to state-of-the-art approaches, the low rank assumption condition with the lifting transform consideration gave good data recovery for every missing ratio. Novelty: The missing data is calculated by lifting polyphase structures by utilizing the available data. The polyphase structures are splitting the value into equivalent multiple triangular matrices, these are processed with the t-SVD to have the better approximation tensor rank.

Keywords: Tensor Completion; Transformbased Optimization; 5/3 Lifting Wavelet Transform; Lowrank tensor completion; tSVD

References

Xue S, Qiu W, Liu F, Jin X. Low-Rank Tensor Completion by Truncated Nuclear Norm Regularization. 2018 24th International Conference on Pattern Recognition (ICPR). 2018;p. 2600–2605. doi: 10.1109/ICPR.2018.8546008
Su Y, Wu X, Liu W. Low-Rank Tensor Completion by Sum of Tensor Nuclear Norm Minimization. IEEE Access. 2019;7:134943–134953. Available from: https://dx.doi.org/10.1109/access.2019.2940664
Zhang L, Song L, Du B, Zhang Y. Nonlocal Low-Rank Tensor Completion for Visual Data. IEEE Transactions on Cybernetics. 2021;51(2):673–685. Available from: https://dx.doi.org/10.1109/tcyb.2019.2910151
Huang H, Liu Y, Liu J, Zhu C. Provable tensor ring completion. Signal Processing. 2020;171:107486. Available from: https://dx.doi.org/10.1016/j.sigpro.2020.107486
Chen L, Jiang X, Liu X, Zhou Z. Logarithmic Norm Regularized Low-Rank Factorization for Matrix and Tensor Completion. IEEE Transactions on Image Processing. 2021;30:3434–3449. Available from: https://dx.doi.org/10.1109/tip.2021.3061908
Liu J, Musialski P, Wonka P, Ye J. Tensor Completion for Estimating Missing Values in Visual Data. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2013;35(1):208–220. Available from: https://dx.doi.org/10.1109/tpami.2012.39
Recht B, Fazel M, Parrilo PA. Guaranteed Minimum-Rank Solutions of Linear Matrix Equations via Nuclear Norm Minimization. SIAM Review. 2010;52(3):471–501. Available from: https://dx.doi.org/10.1137/070697835
Hu Y, Zhang D, Ye J, Li X, He X. Fast and Accurate Matrix Completion via Truncated Nuclear Norm Regularization. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2013;35(9):2117–2130. Available from: https://dx.doi.org/10.1109/tpami.2012.271
Dong J, Xue Z, Guan J, Han ZF, Wang W. Low rank matrix completion using truncated nuclear norm and sparse regularizer. Signal Processing: Image Communication. 2018;68:76–87. Available from: https://dx.doi.org/10.1016/j.image.2018.06.007
Kilmer ME, Martin CD. Factorization strategies for third-order tensors. Linear Algebra and its Applications. 2011;435(3):641–658. Available from: https://dx.doi.org/10.1016/j.laa.2010.09.020
Han ZF, Leung CS, Huang LT, So HC. Sparse and Truncated Nuclear Norm Based Tensor Completion. Neural Processing Letters. 2017;45(3):729–743. Available from: https://dx.doi.org/10.1007/s11063-016-9503-4
Song G, Ng MK, Zhang X. Robust tensor completion using transformed tensor singular value decomposition. Numerical Linear Algebra with Applications. 2020;27(3). Available from: https://dx.doi.org/10.1002/nla.2299
Ganesan T, Rajarajeswari P, Nayak SR, Bhatia AS. A novel genetic algorithm with CDF5/3 filter-based lifting scheme for optimal sensor placement. International Journal of Innovative Computing and Applications. 2021;12(2/3):67. doi: 10.1504/IJICA.2021.113746
Wang JL, Huang TZ, Zhao XL, Jiang TX, Ng MK. Multi-Dimensional Visual Data Completion via Low-Rank Tensor Representation Under Coupled Transform. IEEE Transactions on Image Processing. 2021;30:3581–3596. Available from: https://dx.doi.org/10.1109/tip.2021.3062995
Ding M, Huang TZ, Zhao XL, Ng MK, Ma TH. Tensor train rank minimization with nonlocal self-similarity for tensor completion. Inverse Problems & Imaging. 2021;15(3):475. Available from: https://dx.doi.org/10.3934/ipi.2021001
Kong X, Zhao Y, Chan JCW, Xue J. Hyperspectral Image Restoration via Spatial-Spectral Residual Total Variation Regularized Low-Rank Tensor Decomposition. Remote Sensing. 2022;14(3):511. Available from: https://dx.doi.org/10.3390/rs14030511
Farnaz S, Andrzej C. Image Completion in Embedded Space Using Multistage Tensor Ring Decomposition. 2021;4. Available from: https://doi.org/10.3389/frai.2021.687176
Mittal A, Soundararajan R, Bovik AC. Making a “Completely Blind” Image Quality Analyzer. IEEE Signal Processing Letters. 2013;20(3):209–212. Available from: https://dx.doi.org/10.1109/lsp.2012.2227726
Venkatanath N, Praneeth D, Chandrasekhar BM, Channappayya SS, Medasani SS. Blind image quality evaluation using perception based features. 2015 Twenty First National Conference on Communications (NCC). 2015;p. 1–6. doi: 10.1109/NCC.2015.7084843

Copyright

© 2022 Jyothula & Talari. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Published By Indian Society for Education and Environment (iSee)