Characterizations of the Direct Sum of Two Difference - Mean Fuzzy Graphs

K Radha; S Sri Harini

doi:10.17485/IJST/v17i20.1017

Article

Characterizations of the Direct Sum of Two Difference - Mean Fuzzy Graphs

VIEWS 228
PDF 93

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v17i20.1017

Year: 2024, Volume: 17, Issue: 20, Pages: 2043-2049

Original Article

Characterizations of the Direct Sum of Two Difference - Mean Fuzzy Graphs

K Radha^1*, S Sri Harini²

¹Associate Professor of Mathematics, PG and Research Department of Mathematics, Thanthai Periyar Government Arts and Science College (Autonomous and Affiliated to Bharathidasan University), Trichy-23, Tamil Nadu, India
²Research Scholar, PG and Research Department of Mathematics, Thanthai Periyar Government Arts and Science College (Autonomous and Affiliated to Bharathidasan University), Trichy-23, Tamil Nadu, India

*Corresponding Author
Email: [email protected]

Received Date:04 April 2024, Accepted Date:20 April 2024, Published Date:14 May 2024

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

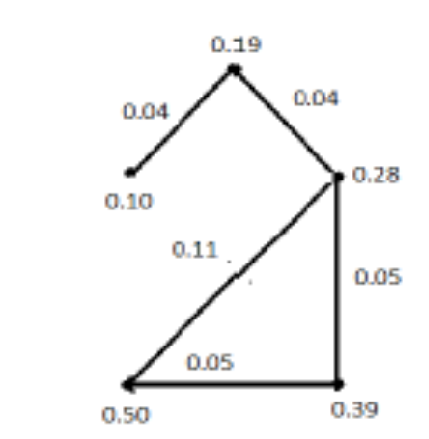
Objectives: This study presents a new type of fuzzy graph known as the difference mean fuzzy graph by introducing difference mean edge. Methodology: In this paper, difference mean edge in a fuzzy graph is defined by considering the relationship between the membership value of the edge and the membership values of its end vertices. Also, difference mean fuzzy graph is defined and its properties are derived. Findings: The difference mean edge and the difference mean fuzzy graph are introduced. The requirements for an edge in the direct sum of two fuzzy graphs to be a difference mean edge are found in this study. Additionally, conditions are derived such that the direct sum of two fuzzy graphs is a difference mean fuzzy graph. Novelty: Depending on the membership values of the edges and vertices, effective edge in fuzzy graph have already been defined. A new concept of difference mean edge in fuzzy graph is introduced. Using this, difference mean fuzzy graph is also introduced. Characterizations of the difference mean edge in the direct sum of fuzzy graphs are attained. The requirements for the necessary and sufficient component of difference mean fuzzy graphs to be a direct sum are suggested. Mathematics Subject Classification (2020): 05C72, 05C76.

Keywords: Difference mean edge, Difference Mean fuzzy graph, Effective fuzzy graph, Effective difference mean edge, Direct sum

References

Zadeh LA. Fuzzy sets. Information and Control. 1965;8(3):338–353. Available from: https://dx.doi.org/10.1016/s0019-9958(65)90241-x
Elumalai A. Recent trends of fuzzy graphs. Malaya Journal of Matematik. 2020;S(2):1618–1621. Available from: https://www.malayajournal.org/articles/MJM0S200431.pdf
Henson T, Santhanalakshmi S. On Direct Sum of Four Fuzzy Graphs. In: International Conference on Mathematical Modeling and Computational Methods in Science and Engineering (ICMMCMSE-2020) , Journal of Physics: Conference Series. (Vol. 1850, pp. 1-14) IOP Publishing. 2021.
Sathavalli N, Biswas S. Recent Trends In Properties And Applications Of Fuzzy Graph. European Chemical Bulletin. 2023;12(8):434–442. Available from: https://www.eurchembull.com/uploads/paper/717733c5cbbd58e5e6270ec01ccdf042.pdf
Radha K, Indumathi P. Properties of Simplicial Vertices in Some Fuzzy Graphs. Advances and Applications in Mathematical Sciences. 2021;20(5):905–916. Available from: https://www.mililink.com/upload/article/1815542614aams_vol_205_march_2021_a19_p905-916__k._radha_and_p._indumati.pdf
Radha K, Renganathan P. Effective fuzzy semigraphs. Advances and Applications in Mathematical Sciences. 2021;20(5):895–904. Available from: https://www.mililink.com/upload/article/775409327aams_vol_205_march_2021_a18_p895-904__k._radha_and_p._renganathan.pdf
Radha K, Uma A. Simplicial Vertices In The Direct Sum, Strong Product, Lexicographic Product And Maximal Product Of Two Fuzzy Graph. Advances and Applications in Mathematical Sciences. 2022;21(6):3357–3369. Available from: https://www.mililink.com/upload/article/281706141aams_vol_216_april_2022_a30_p3357-3369_k._radha_and_a._uma.pdf

Copyright

2024 Radha & Sri Harini. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)