Indian Journal of Science and Technology

Abstract

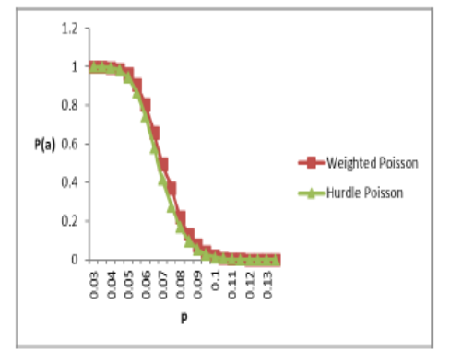
Objectives: Optimizing the sum of risks involved in the selection of acceptance sampling plans playing a vital role. This paper uses the Hurdle Poisson distribution to design an optimal quick switching system attribute plan for a given acceptable quality level (AQL) and limiting quality level (LQL) involving a minimum sum of risks. Methods: The sum of producer's and consumer's risks has been met for the specified AQL and LQL. The sum of these risks, as well as the acceptance and rejection numbers have been calculated using the Hurdle Poisson distribution. The operating characteristic function for the quick switching system attribute plan has also been derived using the Hurdle Poisson distribution. Findings: The producer and the consumer both represent the same party in the final inspection. As a result, the sum of these two risks should be minimized. In this paper, the sum of risks for various operating ratios are tabulated using the Hurdle Poisson distribution. These tabulated values are less than the sum of risks calculated using the Weighted Poisson distribution. Novelty: Reducing the sum of risks is the ultimate aim of the work. In this proposed paper, to attain the minimum sum of risks, the authors make an attempt to approach the Quick Switching System Sampling Plan, when the number of defectives in the submitted lots are very less. In other words, the probability of getting defective is very less. This indicates the quality of the lot selected for the inspection to ensure the protection for the consumer. And the plan is also designed in the way that the producer is also not get affected by rejecting a good lot by the consumer. This is the requirement of minimizing the risks.

Keywords: Acceptable Quality Level (AQL), Limiting Quality Level (LQL), Minimum Risk Plan, Quick Switching System Sampling Attribute Plan, Operating Characteristic (OC) Function, Hurdle Poisson Distribution