Electrically conducting fluid flow with Nanoparticles in an inclined tapering Stenoses Artery through porous medium

K Maruthi Prasad; Prabhaker Reddy Yasa

doi:10.17485/IJST/v13i48.2162

Article

VIEWS 882
PDF 231

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v13i48.2162

Year: 2020, Volume: 13, Issue: 48, Pages: 4708-4722

Original Article

Electrically conducting fluid flow with Nanoparticles in an inclined tapering Stenoses Artery through porous medium

K Maruthi Prasad¹, Prabhaker Reddy Yasa^2*

¹Department of Mathematics, School of Science, GITAM (Deemed to be University), Hyderabad, 502 329, Telangana, India
²Department of BS&H, B V Raju Institute of Technology (BVRIT), Narsapur, 502 313, Telangana, India. Tel.: +91-996-315-9601

*Corresponding Author
Tel: +91-996-315-9601
Email: [email protected]

Received Date:30 November 2020, Accepted Date:22 December 2020, Published Date:04 January 2020

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

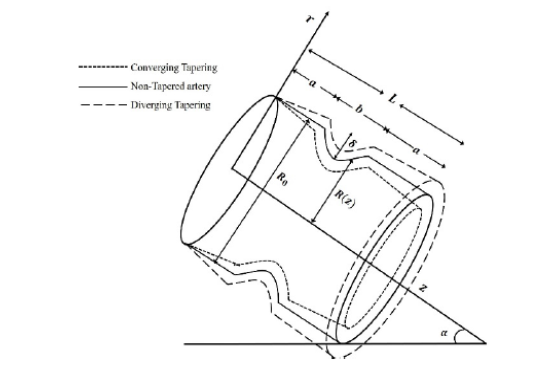
Objectives: A Mathematical Model is built in an inclined tapered artery having permeable walls for a blood flow with nanoparticles through porous media. Methods/Statistical analysis: The Nanoparticle phenomena and Temperature profiles are determined using Homotopy Perturbation Method(HPM). Findings: Analysis on resistance (or) Impedance to the flow and shear stress distribution in the stenotic area with regard to different flow parameters with stenosis height has been estimated by deriving the flow characteristic expressions and the solutions obtained. For various flow parameters, the variations of flow resistance as well as shear stress with stenosis height are illustrated graphically. For study of the fluid flow properties, streamline patterns are also drawn. It is remarkable to take note that, in converging (x < 0), non-tapered (x = 0) and diverging regions (x > 0), the flow patterns aresignificantly impacted by magnetic field existence.

Keywords: Porous medium; tapered artery; Stenosis; Nanofluid; magnetic parameter

References

Padmanabhan N. Mathematical model of arterial stenosis. Medical & Biological Engineering & Computing. 1980;18(3):281–286. Available from: https://dx.doi.org/10.1007/bf02443380
Shukla JB, Parihar RS, Rao BR. Effects of stenosis on non-Newtonian flow of the blood in an artery. Bulletin of Mathematical Biology. 1980;42(3):283–294. Available from: https://doi.org/10.1007/BF02460787
Roy R, Riahi DN, Carrasquero N. Mathematical modeling of blood flow in an artery with an unsteady stenosis using power-law fluid model.
Prasad KM, Yasa PR. Flow of non-Newtonian fluid through a permeable artery having non-uniform cross section with multiple stenosis. Journal of Naval Architecture and Marine Engineering. 2020;17:31–38. Available from: https://dx.doi.org/10.3329/jname.v17i1.40942
Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. Argonne National Lab., IL (United States) 1995.
Prasad KM, Yasa PR. Mathematical Modelling of an Electrically conducting Fluid flow in an Inclined Permeable Tube with Multiple Stenoses. International Journal of Innovative Technology and Exploring Engineering. 2019;9(1):3915–3921.
Sinha A, Misra JC. Influence of Slip Velocity on blood flow through an artery with Permeable Wall: A Theoretical Study. International Journal of Biomathematics. 2012;05(05). Available from: https://dx.doi.org/10.1142/s1793524511001842
Akbar NS, Rahman SU, Ellahi R, Nadeem S. Nano fluid flow in tapering stenosed arteries with permeable walls. International Journal of Thermal Sciences. 2014;85:54–61. Available from: https://dx.doi.org/10.1016/j.ijthermalsci.2014.06.009
Crawford FW, Hoover GM. Flow of fluids through porous mediums. Journal of Geophysical Research. 1966;71(12):2911–2917. Available from: https://dx.doi.org/10.1029/jz071i012p02911
Kasaeian A, Daneshazarian R, Mahian O, Kolsi L, Chamkha AJ, Wongwises S, et al. Nanofluid flow and heat transfer in porous media: A review of the latest developments. International Journal of Heat and Mass Transfer. 2017;107:778–791. Available from: https://dx.doi.org/10.1016/j.ijheatmasstransfer.2016.11.074
Ramamurthy G, Shanker B. Magnetohydrodynamic effects on blood flow through a porous channel. Medical & Biological Engineering & Computing. 1994;32(6):655–659. Available from: https://dx.doi.org/10.1007/bf02524242
El-Shehawey EF, Husseny SZA. Peristaltic transport of a magneto-fluid with porous boundaries. Applied Mathematics and Computation. 2002;129(2-3):421–440. Available from: https://dx.doi.org/10.1016/s0096-3003(01)00054-6
Mandal PK. An unsteady analysis of non-Newtonian blood flow through tapered arteries with a stenosis. International Journal of Non-Linear Mechanics. 2005;40(1):151–164. Available from: https://doi.org/10.1016/j.ijnonlinmec.2004.07.007
Tzirtzilakis EE. A mathematical model for blood flow in magnetic field. Physics of Fluids. 2005;17(7). Available from: https://dx.doi.org/10.1063/1.1978807
Eldesoky IM. Slip effects on the unsteady MHD pulsatile blood flow through porous medium in an Artery under the effect of body acceleration. International Journal of Mathematics and Mathematical Sciences. 2012;2012:1–26. Available from: https://dx.doi.org/10.1155/2012/860239

Copyright

© 2020 Maruthi Prasad & Yasa.This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)