Evolution of Periodic Orbits in the Sun-Jupiter and Sun-Earth Systems

Prashant Kumar; Edapalapati Sai Dhanush Guptha; M Mourya Kishore Raju; V Sri Pranav

doi:10.17485/IJST/v16i10.945

Article

Evolution of Periodic Orbits in the Sun-Jupiter and Sun-Earth Systems

VIEWS 855
PDF 159

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v16i10.945

Year: 2023, Volume: 16, Issue: 10, Pages: 717-726

Original Article

Evolution of Periodic Orbits in the Sun-Jupiter and Sun-Earth Systems

Prashant Kumar^1*, Edapalapati Sai Dhanush Guptha², M Mourya Kishore Raju², V Sri Pranav²

¹Ajeenkya DY Patil University, Pune, India
²Hindustan Institute of Technology, Chennai, India

*Corresponding Author
Email: [email protected]

Received Date:03 May 2022, Accepted Date:23 February 2023, Published Date:10 March 2023

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

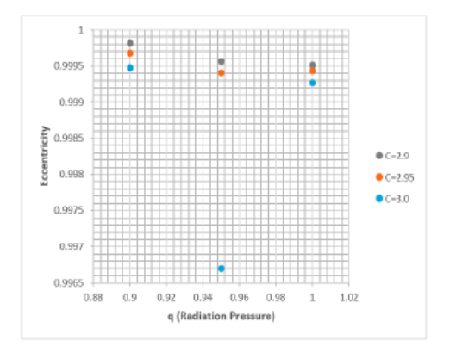
Objective: The periodic orbits around smaller and larger primaries are studied in the Sun-Jupiter and Sun-Earth systems, considering smaller primary as an oblate spheroid. Methods: We used the Poincare surface section method to find the periodic orbits and discussed the differences between these orbits with and without oblateness. Findings: Different trajectories are drawn with the change of Jacobi constant and radiation pressure. Size variations, location, and eccentricity of an orbit around smaller primary are observed due to oblateness effect of the Jupiter and Earth. Oblateness of the smaller primary and radian pressure of the bigger primary have a significant effect on eccentricity, orbit shape, size, and position in phase space. Novelty : Small solar system bodies, such as asteroids and comets in the Sun-Jupiter and Sun-Earth systems, can be explored using periodic orbits. Perturbation caused by oblateness of the smaller primary must be understood and addressed during human exploration missions.

Keywords: Circular Restricted Three Body Problem; Poincare Surface Sections; Jacobi Constant; Radiation Factor; Oblateness; Trajectories; Resonance

References

Koon WS, Lo MW, Marsden JE, Ross SD. Low Energy Transfer to the Moon. Celestial Mechanics and Dynamical Astronomy. 2001;81(1):63–73. Available from: https://doi.org/10.1023/A:1013359120468
Szebehely V, Theory, Orbits. Theory of Orbits. San Diego. Academic Press. 1967.
Darwin G. Periodic Orbits: Scientific Papers. (Vol. 4) Cambridge. Cambridge University Press. 1911.
Moulton F. Periodic Orbits. Carnegie Institute of Washington Publications. 1920;p. 161. Available from: https://archive.org/download/periodicorbitsby00mouluoft/periodicorbitsby00mouluoft.epub
Stromgren EO, Connaissance. Actualle des Orbites dans le Problem des Trois Corps. Publications and Minor communications of Copenhagen Observatory. Astronomical Observatory. 1935;100.
Huang S. Astronomical Journal. 1962;67:304. Available from: https://adsabs.harvard.edu/pdf/1962AJ.....67..304H
Broucke RA. Periodic Orbits in the Restricted Three-Body Problem with Earth-Moon Masses. Technical Report, Jet Propulsion Laboratory, Pasadena . 1968;32. Available from: https://ntrs.nasa.gov/api/citations/19680013800/downloads/19680013800.pdf
Tsirogiannis GA, Douskos CN, Perdios EA. Computation of the Liapunov Orbits in the Photogravitational RTBP with Oblateness. Astrophysics and Space Science. 2006;305(4):389–398. Available from: https://doi.org/10.1007/s10509-006-9171-3
Mittal A, Ahmad I, Bhatnagar KB. Periodic orbits generated by Lagrangian solutions of the restricted three body problem when one of the primaries is an oblate body. Astrophysics and Space Science. 2009;319(1):63–73. Available from: https://doi.org/10.1007/s10509-008-9942-0
Dutt P, Sharma RK. Analysis of Periodic and Quasi-Periodic Orbits in the Earth-Moon System. Journal of Guidance, Control, and Dynamics. 2010;33(3):1010–1017. Available from: http://dx.doi.org/10.2514/1.46400
Dutt P, Sharma RK. Evolution of Periodic Orbits in the Sun-Mars System. Journal of Guidance, Control, and Dynamics. 2011;34(2):635–644. Available from: https://doi.org/10.2514/1.51101
Winter OC, Murray CD. Resonance and chaos: I. First-order interior resonances. Astronomy and Astrophysics. 1997;319(1):290–304. Available from: https://adsabs.harvard.edu/full/1997A%26A...319..290W
Safiya A, Sharma B, RK. Analysis of periodic orbits in the Saturn-Titan system using the method of Poincare section surfaces. Astrophysics and Space Science. 2011;333(1):37–48. Available from: https://doi.org/10.1007/s10509-011-0630-0
Haapala AF, Howell KC. Representations of higher-dimensional Poincaré maps with applications to spacecraft trajectory design. Acta Astronautica. 2014;96:23–41. Available from: https://doi.org/10.1016/j.actaastro.2013.11.019
Prashant K, Sharma RK. Effect of radiation pressure on resonant periodic orbits in photo gravitational restricted three-body problem. International Journal of Mechanical and Production Engineering Research and Development. 2020;10(2):1167–1178. Available from: https://www.semanticscholar.org/paper/EFFECT-OF-RADIATION-PRESSURE-ON-RESONANT-PERIODIC-Kumar-Sharma/ad3476a1f551bbd236ee6776ec9e56007f6641d1
Safiya A, Sharma B, RK. Oblateness effect of Saturn on periodic orbits in the Saturn-Titan restricted three-body problem. Astrophysics and Space Science. 2012;340:245–261. Available from: https://doi.org/ 10.1007/s10509-012-1052-3
Niraj P, Thomas VO. Analysis of Effect of oblateness of smaller primary on the evolution of periodic Orbits. International Journal of Astronomy and Astrophysics. 2016;6:440–463. Available from: http://dx.doi.org/10.4236/ijaa.2016.64036
Bhavika M, Niraj P, Elbaz I. Nonlinear regression multivariate model for first order resonant periodic orbits and error analysis. Planetary and Space Science. 2022;219:105516. Available from: https://doi.org/10.1016/j.pss.2022.105516

Copyright

© 2023 Kumar et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)