Indian Journal of Science and Technology

Abstract

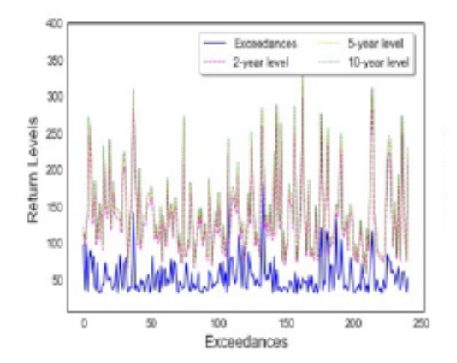
Background/Objectives: Climate change is one of the most challenging problems of recent decades as it is highly volatile and needs a very effective scientific approach to find a solution. Further, the changes in the climate especially extreme cases have a more negative influence on day to day affairs of society. Hence, developed countries pay much attention to climate change and make policies at a global level. To find the scientific solution for these kinds of climate change, Extreme value theory offers effective methods for estimating and quantifying these types of natural hazards associated with climate. Methods: Block (Annual) maxima and peak over threshold are two strategies employed in this theory. The data observed on precipitation are mostly having non-stationary characteristics along with covariates. The generalized extreme value distribution and generalized Pareto distribution are used to model this type of non-stationary stochastic process. Findings: This study proposes a pragmatic automated dual-phase threshold selection technique that employs the entropy method to combine the results from various goodness of fit tests into a single unified measure known as the evaluation indicator, resulting in an efficient threshold for capturing extreme values. This allows for a more comprehensive examination of various thresholds using evaluation indicators and avoids assessing each test criterion individually. Novelty: In contrast to the subjective results of threshold stability plots, the dual-phase technique is based on numerical computations, which reduce bias and improve decision-making objectivity. We illustrate the applicability of the proposed technique by analyzing a precipitation dataset that includes time and wind speed as covariates. The results of the comparative analysis reveal that the proposed automated dual-phase threshold approach outperforms the peaks over threshold and annual maxima methods.

Keywords: Non-stationary, Extreme values, Annual maxima, Threshold selection, Evaluation indicator