Numerical Solution of Non-linear Integro-differential Equations using Operational Matrix based on the Hosoya Polynomial of a Path Graph

P C Jayaprakasha; H C Shashikumar

doi:10.17485/IJST/v16i15.2353

Article

Numerical Solution of Non-linear Integro-differential Equations using Operational Matrix based on the Hosoya Polynomial of a Path Graph

VIEWS 506
PDF 156

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v16i15.2353

Year: 2023, Volume: 16, Issue: 15, Pages: 1159-1167

Original Article

Numerical Solution of Non-linear Integro-differential Equations using Operational Matrix based on the Hosoya Polynomial of a Path Graph

P C Jayaprakasha^1*, H C Shashikumar²

¹Mathematics, Government First Grade College for Women, Tumkur, Karnataka, India
²Mathematics, Government Science College, Hassan, Karnataka, India

*Corresponding Author
Email: j[email protected]

Received Date:22 December 2020, Accepted Date:30 March 2023, Published Date:21 April 2023

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

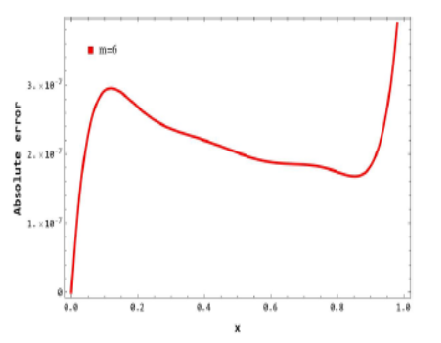
Objectives: Introduction to new numerical techniques to solve differential, difference, and integro-differential equations (IDEs) are always remaining the thrust area of research for many scientists over the centuries. The prime objective of this work is to contribute a new numerical technique to solve IDEs. Method: To address non-linear integro-differential equations, we computed an operational matrix of derivatives based on the Hosoya polynomial of the path graph in this work. Findings: Using the derived operational matrix, we have solved both Volterra and Fredholm integrodifferential equations. Taking suitable examples accuracy of the projected method is demonstrated in this paper in terms of a graphical representation of the absolute error. The results of the examples reveal that the projected method is a suitable method to solve IDEs. Novelty: The application of the Hosoya polynomial of path graph to solve integro-differential equations is a novel approach in the field of numerical analysis. Keywords: Volterra Integrodifferential equations; Fredhlom Integrodifferential equations; Graph theorypolynomials

References

Jalilian R, Tahernezhad T. Exponential spline method for approximation solution of Fredholm integro-differential equation. International Journal of Computer Mathematics. 2020;97(4):791–801. Available from: https://doi.org/10.1080/00207160.2019.1586891
Hamoud AA, Mohammed NM, Ghadle KP, Dhondge SL. Solving Integro differential equation by using numerical techniques. International Journal of Applied Engineering and Research. 2019;14(14):3219–3225. Available from: https://www.ripublication.com/ijaer19/ijaerv14n14_13.pdf
Haq E, Khan AS, Ali M. An efficient approach for solving the linear and nonlinear integro-differential equation. CRPASE. 2020;06(02):104–107. Available from: https://jms.procedia.org/archive/CRPASE_169/CRPASE_procedia_2020_6_2_7.pdf
Kumbinarasaiah S, Mundewadi RA. The new operational matrix of integration for the numerical solution of integro-differential equations via Hermite wavelet. SeMA Journal. 2021;78(3):367–384. Available from: https://doi.org/10.1007/s40324-020-00237-8
Baishya C. An operational matrix based on the Independence polynomial of a complete bipartite graph for the Caputo fractional derivative. SeMA Journal. 2022;79(4):699–717. Available from: https://doi.org/10.1007/s40324-021-00268-9
Ji T, Hou J, Yang C. The operational matrix of Chebyshev polynomials for solving pantograph-type Volterra integro-differential equations. Advances in Continuous and Discrete Models. 2022;2022(1):57. Available from: https://doi.org/10.1186/s13662-022-03729-1
On RHF. Bernoulli Polynomial for the numerical solution of differential equations Anjum Khan, Basit Ali Reshamwale, Sharan Hegde, Sowmya Ashwin Shetty. International Journal of Science, Engineering and Management. 2022;9(3):1–3. Available from: https://www.technoarete.org/common_abstract/pdf/IJSEM/v9/i3/Ext_34705.pdf
Singh AK, Madhulika M, Arora R. Numerical solution of integro-differential equations by using Euler's operational matrix of integration. Science and Aerospace (MESA). 2021;12(2):1–6.
Kurkc¸ UOK, Aslan E, Seizer M. On the numerical solution of fractional differential equations with cubic nonlinearity via matching polynomial of complete graph. Sadhana- Indian Academy of Sciences. 2019;44(246). Available from: https://doi.org/10.1007/s12046-019-1225-7
Raslan KR, Ali KK, Mohamed EMH, Mohamed EMH, salam MAAE. An Operational Matrix Technique Based on Chebyshev Polynomials for Solving Mixed Volterra-Fredholm Delay Integro-Differential Equations of Variable-Order. Journal of Function Spaces. 2022;2022. Available from: https://doi.org/10.1155/2022/6203440
Sadri K, Hosseini K, Mirzazadeh M, Ahmadian A, Salahshour S, Singh J. Bivariate Jacobi polynomials for solving Volterra partial integro‐differential equations with the weakly singular kernel. Mathematical Methods in the Applied Sciences. 2021;p. 1–17. Available from: https://doi.org/10.1002/mma.7662
Hamoud AA, Ghadle KP. Homotopy Analysis Method for the First Order Fuzzy Volterra-Fredholm Integro-differential Equations. Indonesian Journal of Electrical Engineering and Computer Science. 2018;11(3):857–867. Available from: http://doi.org/10.11591/ijeecs.v11.i3.pp857-867
Hamoud AA, Dawood LA, Ghadle KP, Atshan SM. Usage of the modified variational iteration technique for solving Fredholm integro-differential equations. International Journal of Mechanical and Production Engineering Research and Development. 2019;9(2):895–902. Available from: http://dx.doi.org/10.12732/ijam.v33i2.5
Issa MSB, Hamoud AA, Ghadle KP. Numerical solutions of fuzzy integro-differential equations of the second kind. Journal of Mathematics and Computer Science. 2021;23(1):67–74. Available from: http://dx.doi.org/10.22436/jmcs.023.01.07
Cheng AZL, Ali H, Ahmad. Asim Naseem, Maqbool Ahmad Chaudhary, Hosoya and Harary Polynomials of Hourglass and Rhombic Benzenoid Systems. Journal of Chemistry. 2020;2020:1–14. Available from: https://doi.org/10.1155/2020/5398109
Harary F. Graph Theory, Addison Wesley, Reading. 1968.

Copyright

© 2023 Jayaprakasha & Shashikumar. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)