• P-ISSN 0974-6846 E-ISSN 0974-5645

Indian Journal of Science and Technology

Article

Mathematical analysis on anisotropic Bianchi Type-III inflationary string Cosmological models in Lyra geometry
  • VIEWS 1342
  • PDF 303

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v14i1.1705

Year: 2021, Volume: 14, Issue: 1, Pages: 46-54

Original Article

Mathematical analysis on anisotropic Bianchi Type-III inflationary string Cosmological models in Lyra geometry

Baro Jiten1*, Singh Kangujam Priyokumar1,2, Singh T Alexander1

1Department of Mathematical Sciences, Bodoland University, Kokrajhar, 783370, BTR,
Assam, India. Tel.: +919508764687
2Department of Mathematics, Manipur University, Imphal, 795003, Manipur, India

*Corresponding Author
Tel: +919508764687
Email: [email protected]

Received Date:22 September 2020, Accepted Date:20 December 2020, Published Date:11 January 2021

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

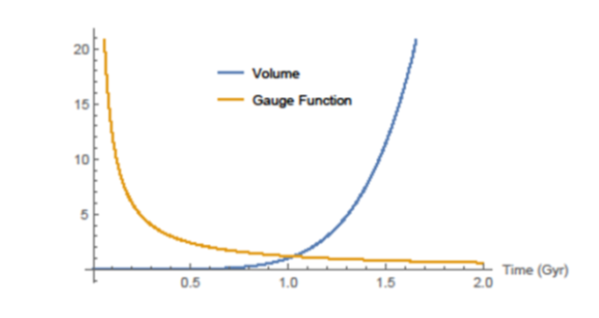
Objectives: To present a new solution to the field equations obtained for Bianchi type-III universe by using the law of variation of H, which yields constant DP. Methods: We study a Bianchi type-III cosmological model with a cloud strings with particles connected to them in Lyra geometry. To find the exact solutions of survival field equations we consider here that the shear scalar and scalar expansion are proportional to each other (saq ) that leads to the equation b = cm and secondly we adopt the assumption considering the Deceleration Parameter q as a negative constant quantity giving the inflationary model. The geometrical and physical properties are studied and compared with the recent observational data. Findings: The present model starts at t=0 with 0 volume and as time progresses it expands with accelerated rate and the model shows that the present universe is particle dominated.

Keywords: Bianchi type III metric; inflation; Lyra geometry; cloud string; anisotropic

References

  1. Stachel J. Thickening the string. I. The string perfect dust. Physical Review D. 1980;21(8):2171–2181. Available from: https://dx.doi.org/10.1103/physrevd.21.2171
  2. Letelier PS. Clouds of strings in general relativity. Physical Review D. 1979;20(6):1294–1302. Available from: https://dx.doi.org/10.1103/physrevd.20.1294
  3. Letelier PS. String cosmologies. Physical Review D. 1983;28(10):2414–2419. Available from: https://dx.doi.org/10.1103/physrevd.28.2414
  4. Kibble TWB. Topology of cosmic domains and strings. Journal of Physics A: Mathematical and General. 1976;9(8):1387–1398. Available from: https://dx.doi.org/10.1088/0305-4470/9/8/029
  5. Kibble TWB. Some implications of a cosmological phase transition. Physics Reports. 1980;67(1):183–199. Available from: https://dx.doi.org/10.1016/0370-1573(80)90091-5
  7. B ZY. Cosmological fluctuations produced near a singularity. Mon. Not. R. Astron.Soc. 1980;192(4):663–667. Available from: https://doi.org/10.1093/mnras/192.4.663
  8. Everett AE. Cosmic strings in unified gauge theories. Physical Review D. 1981;24(4):858–868. Available from: https://dx.doi.org/10.1103/physrevd.24.858
  9. Vilenkin A. Cosmic strings. Physical Review D. 1981;24(8):2082–2089. Available from: https://dx.doi.org/10.1103/physrevd.24.2082
  10. Vilenkin A. Gravitational field of vacuum domain walls and strings. Physical Review D. 1981;23(4):852–857. Available from: https://dx.doi.org/10.1103/physrevd.23.852
  11. Lyra G. U ber eine Modifikation der Riemannschen Geometrie. Mathematische Zeitschrift. 1951;54(1):52–64. Available from: https://dx.doi.org/10.1007/bf01175135
  12. Weyl H. Sitzungsberichte Der Preussischen Akademie Der Wissenschaften. Berlin. Academy Wiss. 1918.
  13. Halford WD. Cosmological theory based on Lyra's Geometry. Australian Journal of Physics. 1970;23(5):863. Available from: https://dx.doi.org/10.1071/ph700863
  14. Bhamra KS. A Cosmological Model of Class One in Lyra's Manifold. Australian Journal of Physics. 1974;27(4):541–547. Available from: https://dx.doi.org/10.1071/ph740541
  15. Beesham A. FLRW Cosmological Models in Lyra's Manifold with Time Dependent Displacement Field. Australian Journal of Physics. 1988;41(6):833. Available from: https://dx.doi.org/10.1071/ph880833
  16. Singh T, Singh GP. Bianchi type‐I cosmological models in Lyra’s geometry. Journal of Mathematical Physics. 1991;32(9):2456–2458. Available from: https://dx.doi.org/10.1063/1.529495
  17. Singh T, Singh GP. Lyra's geometry and cosmology:A review. Fortschr Phys. 1993;41(8):737–764. Available from: https://doi.org/10.1002/prop.2190410804
  18. Rahaman F, Chakraborty S, Bera J. INHOMOGENEOUS COSMOLOGICAL MODEL IN LYRA GEOMETRY. International Journal of Modern Physics D. 2002;11(09):1501–1504. Available from: https://dx.doi.org/10.1142/s0218271802001937
  19. Reddy DRK, Naidu RL, Rao VUM. Axially symmetric cosmic strings in a Scalar-Tensor theory. Astrophysics and Space Science. 2006;306(4):185–188. Available from: https://dx.doi.org/10.1007/s10509-006-9169-x
  20. Reddy DRK, Rao MVS. Axially symmetric string Cosmological model in Brans-Dicke theory of gravitation. Astrophysics and Space Science. 2006;305(2):183–186. Available from: https://dx.doi.org/10.1007/s10509-006-9062-7
  21. Yadav VK, Yadav L, Yadav AK. Bianchi type-III anisotropic universes with a cloud of strings in lyra's geometry. Fizika B. 2010;19(1):29–42. Available from: http://fizika.phy.hr/fizika_b/bv10/b19p029.pdf
  22. Adhav KS, Nimkar AS, Ugale MR, Raut VB. Bianchi type-I cosmological model in Lyra’s manifold. FIZIKA B. 2009;18(2):55–60.
  23. Reddy DRK. Plane symmetric cosmic strings In Lyra manifold. Astrophysics and Space Science. 2005;300(4):381–386. Available from: https://dx.doi.org/10.1007/s10509-005-4716-4
  25. Singh GP, Bishi BK, Sahoo PK. Bianchi type-I bulk viscous cosmology with Chaplygin gas in Lyra Geometry. Chinese Journal of Physics. 2016;54(6):895–905. Available from: https://dx.doi.org/10.1016/j.cjph.2016.10.005
  26. Jesus WDR, Santos AF. On causality violation in Lyra Geometry. International Journal of Geometric Methods in Modern Physics. 2018;15(08). Available from: https://dx.doi.org/10.1142/s0219887818501438
  28. Mollah MR, Singh PK, Singh PS. Bianchi type-III cosmological model with quadratic EoS in Lyra geometry. IJGMMP. 2016;15. Available from: https://doi.org/10.1142/S0219887818501943
  29. Yadav AK, Bhardwaj VK. Lyra’s cosmology of hybrid universe in Bianchi-V space-time. RAA. 2018;18(6):64–72. Available from: https://doi.org/10.1088/1674–4527/18/6/64
  30. Maurya DC, Zia R. Brans-Dicke scalar field cosmological model in Lyra’s geometry. Physical Review D. 2019;100(2):23503–23504. Available from: https://dx.doi.org/10.1103/physrevd.100.023503
  33. Kantowski R, Sachs RK. Some Spatially Homogeneous Anisotropic Relativistic Cosmological Models. Journal of Mathematical Physics. 1966;7(3):443–446. Available from: https://dx.doi.org/10.1063/1.1704952
  34. Kristian J, Sachs RK. Observations in Cosmology. The Astrophysical Journal. 1966;143:379. Available from: https://dx.doi.org/10.1086/148522
  35. Collins CB, Glass EN, Wilkinson DA. Exact spatially homogeneous cosmologies. General Relativity and Gravitation. 1980;12(10):805–823. Available from: https://dx.doi.org/10.1007/bf00763057
  36. Berman MS. A special law of variation for Hubble’s parameter. Il Nuovo Cimento B Series 11. 1983;74(2):182–186. Available from: https://dx.doi.org/10.1007/bf02721676

Copyright

© 2021 Jiten et al.This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)

  • 12 January 2021

Year: 2021, Volume: 14, Issue: 1

Article Metrics


Post Graduate Fellowship in Research Communication

More articles

DON'T MISS OUT!

Subscribe now for latest articles and news.