Solving Neutral Delay Differential Equations Using Galerkin Weighted Residual Method Based on Successive Integration Technique and its Residual Error Correction

C Kayelvizhi; A Emimal Kanaga Pushpam

doi:10.17485/IJST/v17i8.3195

Article

Solving Neutral Delay Differential Equations Using Galerkin Weighted Residual Method Based on Successive Integration Technique and its Residual Error Correction

VIEWS 122
PDF 43

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v17i8.3195

Year: 2024, Volume: 17, Issue: 8, Pages: 732-740

Original Article

Solving Neutral Delay Differential Equations Using Galerkin Weighted Residual Method Based on Successive Integration Technique and its Residual Error Correction

C Kayelvizhi¹, A Emimal Kanaga Pushpam^2*

¹Research Scholar, Department of Mathematics, Bishop Heber College (Autonomous), Affiliated to Bharathidasan University, Tiruchirappalli, 620 017, Tamilnadu, India
²Associate Professor, Department of Mathematics, Bishop Heber College (Autonomous), Affiliated to Bharathidasan University, Tiruchirappalli, 620 017, Tamilnadu, India

*Corresponding Author
Email: [email protected]

Received Date:20 December 2023, Accepted Date:20 January 2024, Published Date:20 February 2024

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

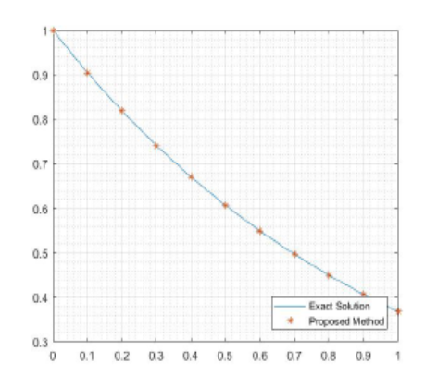
Objectives: The main objectives of this work are to solve Neutral Delay Differential Equations (NDDEs) using Galerkin weighted residual method based on successive integration technique and to obtain the Estimation of Error using Residual function. Methods: The Galerkin weighted residual method based on successive integration technique is proposed to obtain approximate solutions of the NDDEs. In this study, the most widely used classical orthogonal polynomials, namely, the Bernoulli polynomials, the Chebyshev polynomials, the Hermite polynomials, and the Fibonacci polynomials are considered. Findings: Numerical examples of linear and nonlinear NDDEs have been considered to demonstrate the efficiency and accuracy of the method. Approximate solutions obtained by the proposed method are well comparable with exact solutions. Novelty: From the results it is observed that the accuracy of the numerical solutions by the proposed method increases as N increases. The proposed method is very effective, simple, and suitable for solving the linear and nonlinear NDDEs in real-world problems.

Keywords: Galerkin Weighted Residual method, Polynomials, Hermite, Bernoulli, Chebyshev, Fibonacci, Successive integration technique, Neutral Delay Differential Equations

References

Martsenyuk V, Klos-Witkowska A, Dzyadevych S, Sverstiuk A. Nonlinear Analytics for Electrochemical Biosensor Design Using Enzyme Aggregates and Delayed Mass Action. Sensors. 2022;22(3):1–17. Available from: https://doi.org/10.3390/s22030980
Das A, Dehingia K, Sarmah HK, Hosseini K, Sadri K, Salahshour S. Analysis of a delay-induced mathematical model of cancer. Advances in Continuous and Discrete Models. 2022;2022:1–20. Available from: https://doi.org/10.1186/s13662-022-03688-7
Chen-Charpentier B. Delays and Exposed Populations in Infection Models. Mathematics. 2023;11(8):1–22. Available from: https://doi.org/10.3390/math11081919
Domoshnitsky A, Levi S, Kappel RH, Litsyn E, Yavich R. Stability of neutral delay differential equations with applications in a model of human balancing. Mathematical Modelling of Natural Phenomena. 2021;16(21):1–18. Available from: https://doi.org/10.1051/mmnp/2021008
Loucif S, Guefaifia R, Zitouni S, Khochemane HE. Global well-posedness and exponential decay of fully dynamic and electrostatic or quasi-static piezoelectric beams subject to a neutral delay. Zeitschrift für angewandte Mathematik und Physik. 2023;74(3):1–22. Available from: https://doi.org/10.1007/s00033-023-01972-4
Shaalini JV, Pushpam AEK. Analysis of Composite Runge Kutta Methods and New One-Step Technique for Stiff Delay Differential Equations. IAENG International Journal of Applied Mathematics. 2019;49(3):1–10. Available from: https://www.iaeng.org/IJAM/issues_v49/issue_3/IJAM_49_3_14.pdf
Ismail NIN, Majid ZA, Senu N. Hybrid Multistep Block Method for Solving Neutral Delay Differential Equations. Sains Malaysiana. 2020;49(4):929–940. Available from: https://www.ukm.my/jsm/pdf_files/SM-PDF-49-4-2020/22.pdf
Jafari H, Mahmoudi M, Noori skandari MH. A new numerical method to solve pantograph delay differential equations with convergence analysis. Advances in Difference Equations. 2021;2021(1):1–12. Available from: https://doi.org/10.1186/s13662-021-03293-0
Mohammad M, Trounev A. A New Technique for Solving Neutral Delay Differential Equations Based on Euler Wavelets. Complexity. 2022;2022:1–8. Available from: https://doi.org/10.1155/2022/1753992
Yuzbasi S, Tamar ME. A new approaching method for linear neutral delay differential equations by using Clique polynomials. Turkish Journal of Mathematics. 2023;47(7):2098–2121. Available from: https://journals.tubitak.gov.tr/cgi/viewcontent.cgi?article=3481&context=math#:~:text=using%20a%20truncated%20series%20expansion,system%20of%20linear%20algebraic%20equations.
Kayelvizhi C, Pushpam AEK. Application of Polynomial Collocation Method Based on Successive Integration Technique for Solving Delay Differential Equation in Parkinson’s Disease. Indian Journal Of Science And Technology. 2024;17(2):112–119. Available from: https://doi.org/10.17485/IJST/v17i2.2573
Jiang K, Huang Q, Xu X. Discontinuous Galerkin Methods for Multi-Pantograph Delay Differential Equations. Advances in Applied Mathematics and Mechanics. 2020;12(1):189–211. Available from: https://doc.global-sci.org/uploads/Issue/AAMM/v12n1/121_189.pdf?code=1IBB99GZdzOztNjb2EMVmQ%3D%3D#:~:text=The%20discontinuous%20Galerkin%20(DG)%20method,and%20integral%20dif%2D%20ferential%20equations.
Saray BN, Lakestani M. On the sparse multi-scale solution of the delay differential equations by an efficient algorithm. Applied Mathematics and Computation. 2020;381:125291. Available from: https://doi.org/10.1016/j.amc.2020.125291
Yuzbasi S, Karacayir M. Galerkin-like method for solving linear functional differential equations under initial conditions. Turkish Journal of Mathematics. 2020;44(1):85–97. Available from: https://journals.tubitak.gov.tr/cgi/viewcontent.cgi?article=1350&context=math#:~:text=We%20consider%20the%20problem%20with,degree%20N%20of%20our%20choice.

Copyright

© 2024 Kayelvizhi & Pushpam. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)