Some New Classes of (k, d) Graceful 3 Distance Trees and 3 Distance Unicyclic Graphs

Gobind Mohanty; Debdas Mishra; Pravat Sarangi; Subarna Bhattacharjee

doi:10.17485/IJST/v15i14.254

Article

Some New Classes of (k, d) Graceful 3 Distance Trees and 3 Distance Unicyclic Graphs

VIEWS 1287
PDF 180

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v15i14.254

Year: 2022, Volume: 15, Issue: 14, Pages: 630-639

Original Article

Some New Classes of (k, d) Graceful 3 Distance Trees and 3 Distance Unicyclic Graphs

Gobind Mohanty¹, Debdas Mishra², Pravat Sarangi³, Subarna Bhattacharjee^1*

¹Department of Mathematics, Ravenshaw University, Cuttack, Odisha, India
²Former Professor, C.V. Raman College of Engineering, Bhubaneswar, Odisha, India
³Department of Statistics, Ravenshaw University, Cuttack, Odisha, India

*Corresponding Author
Email: [email protected]

Received Date:30 January 2022, Accepted Date:04 March 2022, Published Date:11 April 2022

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

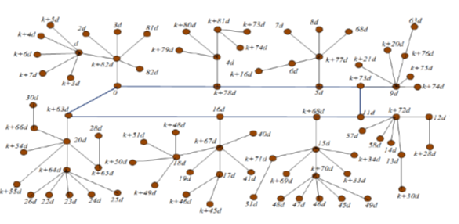
Objectives: To identify a new family of (k; d) graceful graphs. Methods : The methodology involves mathematical formulation for labeling of the vertices of a given graph and subsequently establishing that these formulations give rise to (k;d) graceful labeling. Findings: Here we define a three-distance tree as the tree possessing a path such that each vertex of the tree is at most at a distance three from that path. In this paper we identify two families of three distance trees that possess (k; d) graceful labeling. Furthermore, we show that the three distance unicyclic graphs obtained from these three distance trees by joining two end vertices of their central paths are also (k; d) graceful. Novelty: Here, we give (k; d) graceful labeling to two new families of graphs, namely some classes of three distance trees and three distance unicyclic graphs. This effort is the first of its kind which involves exploration of 3-distance (k; d) graceful graphs.

Keywords: (k; D); graceful labelling; Hairy cycle; Firecracker; Three distance tree; Three distance unicyclic graphs

References

Acharya BD, Hegde SM. Arithmetic graphs. Journal of Graph Theory. 1990;14(3):275–299. Available from: https://dx.doi.org/10.1002/jgt.3190140302
Gallian JA. A dynamic survey of graph labeling. Electronic Journal of Combinatorics. 2021. Available from: http://www.combinatorics.org/Surveys/
Hegde SM, Shetty S. Sequential and magic labeling of a class of trees. National Academy of Science Letters. 2001;24:137–141. Available from: https://www.researchgate.net/profile/Suresh-Hegde/publication/266240373_Sequential_and_magic_labeling_of_a_class_of_trees/links/5f1477d7299bf1e548c37269/Sequential-and-magic-labeling-of-a-class-of-trees.pdf
SM, Murugan K. Pentagonal Graceful Labeling of Some Graphs. World Scientific News. 2021;155:98–112. Available from: http://www.worldscientificnews.com/wp-content/uploads/2021/02/WSN-155-2021
Kumar S, Sriraj MA, Hegde SM. Hegde, graceful labeling of digraphs-a survey. AKCE InternationalJournal of Graphs and Combinatorics. 2021;18:143–147. Available from: https://doi.org/10.1080/09728600.2021.1978014
Sankari RS, Nisaya MPSA. Higher order triangular graceful labeling of some graphs. World Scientific News. 2021;156:40–61. Available from: http://www.worldscientificnews.com/wp-content/uploads/2021/03/WSN-156-2021-40-61.pdf.
Deen MRZE, GE. New classes of graphs with edge δ− graceful labeling. AIMS Mathematics. 2022;7:3554–3589. doi: 10.3934/math.2022197
Kanani JC, Kaneria VJ. Graceful labeling for some snake related graphs. Ganita. 2021;71(1):243–255. Available from: https://bharataganitaparisad.com/wp-content/uploads/2021/10/711-ch025.pdf
Yeh RK. A note on n-set distance-labelings of graph. Open Journal of Discrete Mathematics. 2021;11(03):55–60. doi: 10.4236/ojdm.2021.113005
Kumar A, Kumar A, Kumar V, Kumar K. Graceful distance labeling for some particular graphs. Malaya Journal of Matematik. 2021;9(1):557–561. Available from: https://dx.doi.org/10.26637/mjm0901/0094

Copyright

© 2022 Mohanty et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Published By Indian Society for Education and Environment (iSee)