AMST: Accelerated Minimum Spanning Tree for Scalable Data

Chittaranjan Mohapatra; Nibedita Adhikari; B N Bhramar Ray; Biswojit Nayak; Akshaya Kumar Dash

doi:10.17485/IJST/v16i37.1420

Article

AMST: Accelerated Minimum Spanning Tree for Scalable Data

VIEWS 326
PDF 73

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v16i37.1420

Year: 2023, Volume: 16, Issue: 37, Pages: 3110-3120

Original Article

AMST: Accelerated Minimum Spanning Tree for Scalable Data

Chittaranjan Mohapatra^1,2*, Nibedita Adhikari¹, B N Bhramar Ray¹, Biswojit Nayak¹, Akshaya Kumar Dash^2,1

¹Silicon Institute of Technology, Patia, Bhubaneswar, Odisha, India
²Utkal University, Vani Vihar, Bhubaneswar, Odisha, India

*Corresponding Author
Email: [email protected]

Received Date:31 August 2023, Accepted Date:05 September 2023, Published Date:03 October 2023

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

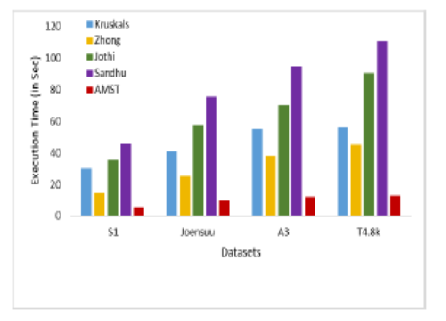
Objectives: A traditional Minimum Spanning Tree (MST) is quite complex for large datasets concerning time and space complexities. So an Accelerated MST (AMST) is proposed for scalable data. Methods: AMST uses the k-means clustering to divide large data into a bunch of small-size data. The Delaunay Triangulation is applied to find the relationship among the data in O(nlogn) time for n points as compared to earlier approaches. A mid-point heuristic is designed to combine all clustered MSTs to get the MST for the original data. A refinement process is used for any mislaid of minimum weight edges. Findings: Several desirable properties of the AMST have been developed and compared with the results of existing literature. AMST is quite competitive in terms of time complexities, least weight error rate and accuracy for both large and small-size datasets. The mathematical analysis of the time complexity O(nlogn) proves that the proposed AMST has a 95% faster execution time than others. The proposed AMST has the least Weight Error Rate than other approaches which indicates that the cost is close to the exact Algorithms. The accuracy of the AMST is an average of 93% in different clustering accuracy indices which is similar to other approaches. Novelty: The execution time and accuracy prove that a faster MST can be developed to construct pins wire length routing in the promising field of VLSI (Very Large-Scale Integration) physical design.

Keywords: MST; Clustering; Delaunay Triangulation; Minimax Distance; Spectral Clustering; MidPoint Heuristic

References

Jothi R, Mohanty SK, Ojha A. Fast approximate minimum spanning tree based clustering algorithm. Neurocomputing. 2018;272:542–557. Available from: https://doi.org/10.1016/j.neucom.2017.07.038
Sandhu SS, Tripathy BK, Jagga S. KMST+: A K-Means++-Based Minimum Spanning Tree Algorithm. Smart Innovations in Communication and Computational Sciences. 2019;p. 113–127. Available from: https://doi.org/10.1007/978-981-10-8968-8_10
Khan A, Aesha AA, Sarker J. A New Algorithmic Approach to Finding Minimum Spanning Tree. 2018 4th International Conference on Electrical Engineering and Information & Communication Technology (iCEEiCT). 2018;p. 590–594. Available from: https://doi.org/10.1109/CEEICT.2018.8628095
Mishra G, Mohanty SK. A fast hybrid clustering technique based on local nearest neighbor using minimum spanning tree. Expert Systems with Applications. 2019;132:28–43. Available from: https://doi.org/10.1016/j.eswa.2019.04.048
Berg MD, Kreveld MV, Overmars M, Schwarzkopf O. Computational Geometry: algorithms and applications . (Vol. 2) 1997.
Funke D, Sanders P, Winkler V. Load-Balancing for Parallel Delaunay Triangulations. Lecture Notes in Computer Science. 2019;p. 156–169. Available from: https://doi.org/10.1007/978-3-030-29400-7_12
Nguyen CM, Rhodes PJ. Delaunay triangulation of large-scale datasets using two-level parallelism. Parallel Computing. 2020;98:102672. Available from: https://doi.org/10.1016/j.parco.2020.102672
Sharp N, Gillespie M, Crane K. Geometry processing with intrinsic triangulations. ACM SIGGRAPH 2021 Courses. 2021. Available from: https://doi.org/10.1145/3450508.3464592
Mikhailov V, Pchenitchnyi P, Tagirov R, Khabibrakhmanov R, Shaimukhametov R. Analysis of algorithms for implementing Delaunay triangulation. 2021 International Conference on Information Technology and Nanotechnology (ITNT). 2021;p. 1–5. Available from: https://doi.org/10.1109/ITNT52450.2021.9649039
Mathieson L, Moscato P. An Introduction to Proximity Graphs. Business and Consumer Analytics: New Ideas. 2019;p. 213–233. Available from: https://doi.org/10.1007/978-3-030-06222-4_4
Ahmed M, Seraj R, Islam SMS. The k-means Algorithm: A Comprehensive Survey and Performance Evaluation. Electronics. 2020;9(8):1295. Available from: https://doi.org/10.3390/electronics9081295
Wu G, Xu Y, Wu D, Ragupathy M, Mo YY, Chu C. Flip-flop clustering by weighted K-means algorithm. Proceedings of the 53rd Annual Design Automation Conference. 2016;p. 1–6. Available from: https://doi.org/10.1145/2897937.2898025
Inaba M, Katoh N, Imai H. Applications of weighted Voronoi diagrams and randomization to variance-based k-clustering. Proceedings of the tenth annual symposium on Computational geometry - SCG '94. 1994;p. 332–339. Available from: https://doi.org/10.1145/177424.178042
Germiniani S, Pravadelli G. Exploiting clustering and decision-tree algorithms to mine LTL assertions containing non-boolean expressions. 2022 IFIP/IEEE 30th International Conference on Very Large Scale Integration (VLSI-SoC). 2022;p. 1–6. Available from: https://doi.org/10.1109/VLSI-SoC54400.2022.9939640
Zhong C, Malinen M, Miao D, Fränti P. A fast minimum spanning tree algorithm based on K-means. Information Sciences. 2015;295:1–17. Available from: https://doi.org/10.1016/j.ins.2014.10.012
Miller SJ. A probabilistic proof of Wallis's formula for π. 2008. Available from: https://doi.org/10.1080/00029890.2008.11920586
Franti P, Sieranoja S. K-means properties on six clustering benchmark datasets . 2018. Available from: http://cs.uef.fi/sipu/datasets/
Anita R, Subalalitha CN. An Approach to Cluster Tamil Literatures Using Discourse Connectives. 2019 IEEE 1st International Conference on Energy, Systems and Information Processing (ICESIP). 2019;p. 1–4. Available from: https://doi.org/10.1109/ICESIP46348.2019.8938315
Radu RG, Radulescu IM, Truica CO, Apostol ES, Mocanu M. Clustering Documents using the Document to Vector Model for Dimensionality Reduction. 2020 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR). 2020;p. 1–6. Available from: https://doi.org/10.1109/AQTR49680.2020.9129967
Mishra S, Moulik S, Prakash V. Invalid Scenarios of External Cluster Validity Indices: An Analysis Using Bell Polynomial. 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC). 2021;p. 2215–2220. Available from: https://doi.org/10.1109/SMC52423.2021.9659242
Kim KH, Choi S. Neighbor search with global geometry: a minimax message passing algorithm. Proceedings of the 24th international conference on machine learning. 2007;p. 401–408. Available from: https://doi.org/10.1145/1273496.1273547
Chehreghani MH. Efficient Computation of Pairwise Minimax Distance Measures. 2017 IEEE International Conference on Data Mining (ICDM). 2017;p. 799–804. Available from: https://doi.org/10.1109/ICDM.2017.95
Yang Y, Shen F, Huang Z, Shen HT, Li X. Discrete Nonnegative Spectral Clustering. IEEE Transactions on Knowledge and Data Engineering. 2017;29(9):1834–1845. Available from: https://doi.org/10.1109/TKDE.2017.2701825

Copyright

© 2023 Mohapatra et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)