Indian Journal of Science and Technology

Abstract

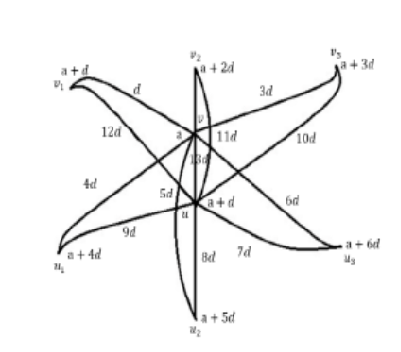
Objectives: To identify a new family of arithmetic sequential graceful graphs. Methods : The methodology involves mathematical formulation for labeling of the vertices of a given graph and subsequently establishing that these formulations give rise to arithmetic sequential graceful labeling. Findings: Here, we introduce the square graph , which shares its vertex set with G. In , two vertices are considered adjacent if their distance in is either 1 or 2. To further elucidate, we identify the splitting graph as an extension of G. Specifically, for each vertex in G, we introduce a corresponding new vertex . Additionally, we demonstrate the construction of the W-star graph. This graph is formed by connecting the apex vertex of the 1st star graph to the apex vertex of the 2nd star graph through a path of length 3. Subsequently, we connect the apex vertex of the 2nd star graph to the apex vertex of the 3rd star graph, also via a path of length 3. Novelty: Here we give arithmetic sequential graceful labeling to a new family of graphs, namely W-star, Square of graph G, splitting graph, Banana tree and proved that these graphs possess arithmetic sequential graceful labeling.

Keywords: Star graph, W­star, Square of graph G, Splitting graph, Banana tree, Graceful labeling