Formation of Repetitive Group Sampling Plan for Life Tests Based on Percentiles using Odd Frechet Inverse Rayleigh Distribution

P K Neena Krishna; S Jayalakshmi

doi:10.17485/IJST/v17i21.502

Article

Formation of Repetitive Group Sampling Plan for Life Tests Based on Percentiles using Odd Frechet Inverse Rayleigh Distribution

VIEWS 78
PDF 26

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v17i21.502

Year: 2024, Volume: 17, Issue: 21, Pages: 2232-2239

Original Article

Formation of Repetitive Group Sampling Plan for Life Tests Based on Percentiles using Odd Frechet Inverse Rayleigh Distribution

P K Neena Krishna^1*, S Jayalakshmi²

¹Guest Lecturer, BJCSI College, Mulayara, Thiruvananthapuram, Kerala, India
²Assistant Professor, Department of Statististics, Bharathiar University, Coimbatore, TamilNadu, India

*Corresponding Author
Email: [email protected]

Received Date:21 February 2024, Accepted Date:29 April 2024, Published Date:29 May 2024

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

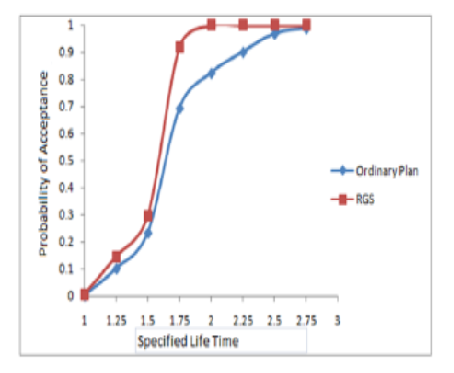
Objectives: This paper presents the idea of Repetitive Group Sampling Plans using Odd Frechet Inverse Rayleigh Distribution, when the life test is truncated at a pre-specified time. The main objective of the proposed sampling plan is to minimize the sample size because the analogous inspection time and inspection cost will be reduced. Methods: A truncated life test may be conducted to evaluate the smallest sample size to insure certain percentile lifetime of products. The minimum sample size and its ratio for the specified lifetime percentile were derived for the producer’s risk. The operating characteristic values are also obtained for the proposed sampling plan. The corresponding table values are obtained through Monto Carlo Simulation technique. Findings: The results from the sampling plan developed in this research can easily be adaptable in practical situation with small sample sizes and fewer experimental times and hence the plan yields a better result for reliability sampling plan. Novelty: The work designed and developed with the aim that sampling plan in this paper may be helpful for the engineers and statistical plan developers in the field of statistical quality control especially in attribute reliability sampling plan. The tables are generated which is useful for both producer and consumer. This plan can highly recommendable since the products are randomly sampled and also the procedure for sampling involves less experiment time and with minimum sample size.

Keywords: Odd Frechet Inverse Rayleigh Distribution, Percentiles, Repetitive Group Sampling Plan (RGS), Producer’s risk

References

Al-Omari A, Al-Nasser A, Ciavolino E. Acceptance sampling plans based on truncated life tests for Rama distribution. International Journal of Quality & Reliability Management. 2019;36(7):1181–1191. Available from: https://dx.doi.org/10.1108/ijqrm-04-2018-0107
Farouk M, Aziz N, Zain Z. A time-truncated life test approach on the new two-sided group chain sampling plan with log-logistic distribution. International Journal of Supply Chain Management. 2019;8(4):1059–1063. Available from: https://ojs.excelingtech.co.uk/index.php/IJSCM/article/view/3447/1866
Goual H, Yousof HM. Validation of Burr XII inverse Rayleigh model via a modified chi-squared goodness-of-fit test. Journal of Applied Statistics. 2020;47(3):393–423. Available from: https://dx.doi.org/10.1080/02664763.2019.1639642
Jayalakshmi S, Krishna PKN. Designing of Special Type Double Sampling Plan for Life Tests Based on Percentiles Using Exponentiated Frechet Distribution. Reliability Theory & Applications. 2021;16(1):117–123. Available from: https://www.gnedenko.net/Journal/2021/012021/RTA_1_2021-11.pdf
Lee AHI, Wu CW, Liu SW, Liu CH. Designing acceptance sampling plans based on the lifetime performance index under gamma distribution. The International Journal of Advanced Manufacturing Technology. 2021;115:3409–3422. Available from: https://doi.org/10.1007/s00170-021-07299-6
Tripathi H, Dey S, Saha M. Double and group acceptance sampling plan for truncated life test based on inverse log-logistic distribution. Journal of Applied Statistics. 2021;48(7):1227–1242. Available from: https://dx.doi.org/10.1080/02664763.2020.1759031
Ibrahim S, Zoramawa AB, Dauran NS, Hamza MM, Suru DS. A Study on Extension of Double Acceptance Sampling Plans Based on Truncated Life Tests on The Inverse Rayleigh Distribution. Iconic Research and Engineering Journals. 2021;5(5):155–182. Available from: https://www.irejournals.com/formatedpaper/17029742.pdf
Aziz N, Hasim Z, Zain Z. Two-Sided Group Chain Sampling Plans Based on Truncated Life Test for Generalized Exponential Distribution. Mathematics and Statistics. 2021;9(4):439–444. Available from: https://dx.doi.org/10.13189/ms.2021.090404
Babu MS, Rao GS, Rosaiah K. Double-Acceptance Sampling Plan for Exponentiated Fréchet Distribution with Known Shape Parameters. Mathematical Problems in Engineering. 2021;2021:1–9. Available from: https://dx.doi.org/10.1155/2021/7308454
Jayalakshmi S, Krishna PKN. Designing of Double Sampling Plan for Truncated Life Tests Based on Percentiles using Kumaraswamy Exponentiated Rayleigh Distribution. International Journal of Mathematics Trends and Technology. 2022;68(1):29–35. Available from: https://dx.doi.org/10.14445/22315373/ijmtt-v68i1p503
Jayalakshmi S, Vijilamery S. Designing of Special Type Double Sampling Plan for Truncate Life Test using Gompertz Frechet Distribution. International Journal of Mathematics Trends and Technology. 2022;68(1):70–76. Available from: https://dx.doi.org/10.14445/22315373/ijmtt-v68i1p508
Umamaheshwari P, Veerakumari KP, Suganya S. Selection Procedure For Skip Lot Sampling Plan Of Type Sksp-R Based On Percentiles Of Exponentiated Rayleigh Distribution. Reliability Theory & Applications. 2023;18(1):432–439. Available from: https://gnedenko.net/Journal/2023/012023/RTA_1_2023-34.pdf
Aziz N, Fei SW, Hafeez W, Shaharudin SM, Shabbir J. A Time Truncated New Group Chain Sampling Plan Based on Log-Logistic Distribution. Mathematics and Statistics. 2023;11(3):548–557. Available from: https://dx.doi.org/10.13189/ms.2023.110311
Devaarul S, Jothimani K. Design and development of relational repetitive group sampling plans - (RRGS - 1) International Journal of Statistics and Applied Mathematics. 2020;5(5, Part B):104–107. Available from: https://dx.doi.org/10.22271/maths.2020.v5.i5b.588
Shafqat A, Huang Z, Aslam M. Design of X-bar control chart based on Inverse Rayleigh Distribution under repetitive group sampling. Ain Shams Engineering Journal. 2021;12(1):943–953. Available from: https://dx.doi.org/10.1016/j.asej.2020.06.001
Elgarhy M, Alrajhi S. The odd Fréchet inverse Rayleigh distribution: statistical properties and applications. Journal of Nonlinear Sciences and Applications. 2018;12(5):291–299. Available from: https://dx.doi.org/10.22436/jnsa.012.05.03
Haq MAu, Elgarhy M. The Odd Frѐchet-G Family of Probability Distributions. Journal of Statistics Applications & Probability. 2018;7(1):189–203. Available from: https://dx.doi.org/10.18576/jsap/070117

Copyright

© 2024 Krishna & Jayalakshmi. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)