Indian Journal of Science and Technology

Abstract

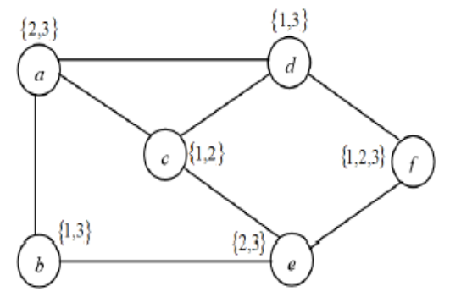
Background/Objectives: List coloring problem is one of the most important generalizations of well-known graph coloring problem. List coloring of a graph is a problem of assigning colors to all vertices of the graph from a pre-defined list of colors for every vertex in such a way that no two adjacent vertices share the same color. In this process, the highest color assigned to a vertex is called span. The objective of the list coloring problem is to minimize this span. Methods: In this study, two heuristic methods are proposed to solve this problem namely: a greedy randomize adaptive search heuristic and a simple greedy heuristic. Findings: Computational experiments on randomly generated graphs show that both the proposed heuristics are capable of obtaining optimal results. It is also observed that greedy randomize adaptive search heuristic performed well as compared to the other one. Comparison with other state-of-art algorithms reveals that both the proposed heuristics have obtained better results for larger graphs in a reasonable time. Novelty: The origin of list coloring problem is very old, still its solving procedures are limited to mostly exact algorithms. Moreover, there is no heuristic available for LCP for general graphs having vertex size more than 150. This paper is an attempt to develop heuristics/metaheuristics for solving this problem for larger graphs in a reasonable time which is not possible with exact methods.

Keywords: Graph Coloring, List coloring, GRASP