Numerical Solution of Subdiffusion Bioheat equation with Single Phase lag

Jagdish Sonawane; Bhausaheb Sonatakke; Kalyanrao Takale

doi:10.17485/IJST/v17i11.3220

Article

Numerical Solution of Subdiffusion Bioheat equation with Single Phase lag

VIEWS 339
PDF 99

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v17i11.3220

Year: 2024, Volume: 17, Issue: 11, Pages: 955-966

Original Article

Numerical Solution of Subdiffusion Bioheat equation with Single Phase lag

Jagdish Sonawane^1*, Bhausaheb Sonatakke², Kalyanrao Takale³

¹Department of Mathematics, GES R. H. Sapat College of Engineering, Management and Research, Nashik, Maharashtra, India
²Department of Mathematics, Pratishthan Mahavidyalaya, Paithan, Aurangabad, Maharshtra, India
³Department of Mathematics, RNC Arts, JDB Commerce and NSC Science College, Nashik Road, Nashik, Maharashtra, 422101, India

*Corresponding Author
Email: [email protected]

Received Date:23 December 2023, Accepted Date:12 February 2024, Published Date:28 February 2024

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

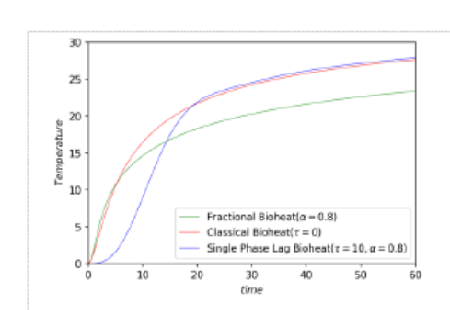
Objectives: The aim of this study is to investigate thermal beheviour of living tissues, for this we use subdiffusion bioheat equation with single phase lag model. Methods: The Crank-Nicolson finite difference scheme is used for subdiffusion bioheat equation with single phase lag by using Caputo fractional derivative. A Python program is used to calculate a numerical solution, which is then visually depicted through graphical representation. Finding: We discuss significance of heat flux time relaxation parameter and fractional parameter. To explore our findings, we conducted comparative analysis of subdiffusion bioheat equation with single phase lag model with classical bioheat model and fractional bioheat model. Moreover, We discussed stability and convergence of developed scheme. Novelty: The bio heat equation can be effectively addressed using the Crank-Nicolson finite difference method of fractional-order. Developed Python program provides effective tool for getting numerical solution of fractional differential equation. Single phase lag model is useful for short time heating process.

Keywords: Fractional Differential Equation, Caputo fractional derivatives, Subdiffusion bioheat equation, Single Phase Lag, Python etc

References

Hristov J, Bio. Bio-Heat Models Revisited: Concepts, Derivations, Nondimensalization and Fractionalization Approaches. Frontiers in Physics. 2019;7. Available from: https://doi.org/10.3389/fphy.2019.00189
Siedlecka U, Ciesielski M. Analysis of solutions of the 1D fractional Cattaneo heat transfer equation. Journal of Applied Mathematics and Computational Mechanics. 2021;20(4):87–98. Available from: https://doi.org/10.17512/jamcm.2021.4.08
Zhou H, Li P, Fang Y. Single-phase-lag thermoelastic damping models for rectangular cross-sectional micro- and nano-ring resonators. International Journal of Mechanical Sciences. 2019;163:105132. Available from: https://doi.org/10.1016/j.ijmecsci.2019.105132
Nikan O, Avazzadeh Z, Machado JAT. Numerical approach for modeling fractional heat conduction in porous medium with the generalized Cattaneo model. Applied Mathematical Modelling. 2021;100:107–124. Available from: https://doi.org/10.1016/j.apm.2021.07.025
Goudarzi P, Azimi A. Numerical simulation of fractional non-Fourier heat conduction in skin tissue. Journal of Thermal Biology. 2019;84:274–284. Available from: https://doi.org/10.1016/j.jtherbio.2019.05.021
Kolade M, Owolabi A, Atangana A, Akgul. Modelling and analysis of fractal-fractional partial differential equations: Application to reaction-diffusion model. Alexandria Engineering Journal. 59. Available from: https://doi.org/10.1016/j.aej.2020.03.022
Takale KC. Numerical method for Time Fractional Bio heat Transfer Equation and Applications. Int J Res Anal Rev. 2019;6:1301–1307. Available from: http://ijrar.org/viewfull.php?&p_id=IJRAR19J2367
Patil HM, Maniyeri R. Finite difference method based analysis of bio-heat transfer in human breast cyst. Thermal Science and Engineering Progress. 2019;10:42–47. Available from: https://doi.org/10.1016/j.tsep.2019.01.009
Qiao Y, Wang X, Qi H, Xu H. Numerical simulation and parameters estimation of the time fractional dual-phase-lag heat conduction in femtosecond laser heating. International Communications in Heat and Mass Transfer. 2021;125:105355. Available from: https://doi.org/10.1016/j.icheatmasstransfer.2021.105355
Abbas I, Abdalla A, Anwar F, Sapoor H. A numerical solution of 2-D single-phase-lag (SPL) bio-heat model using alternating direction implicit (ADI) finite difference method. Sohag Journal of Sciences. 2022;0(0). Available from: https://doi.org/10.21608/sjsci.2022.154607.1020
Zhang Q, Sun Y, Yang J. Bio-heat response of skin tissue based on three-phase-lag model. Scientific Reports. 2020;10(1):6421. Available from: https://doi.org/10.1038/s41598-020-73590-3
Sonawane J, Sontakke B, Takale K. Approximate Solution of Sub diffusion Bio heat Transfer Equation. Baghdad Science Journal. 2023;20(1(SI)):394. Available from: https://bsj.uobaghdad.edu.iq/index.php/BSJ/article/view/8410
Kharde U, Takale K, Gaikwad S. Numerical solution of time fractional drug concentration equation in central nervous system. Journal of Mathematical and Computational Science. 2021;11(6):7317–7336. Available from: https://doi.org/10.28919/jmcs/6470
Mozafarifard M, Toghraie D. Time-fractional subdiffusion model for thin metal films under femtosecond laser pulses based on Caputo fractional derivative to examine anomalous diffusion process. International Journal of Heat and Mass Transfer. 2020;153:119592. Available from: https://doi.org/10.1016/j.ijheatmasstransfer.2020.119592

Copyright

© 2024 Sonawane et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)