Plane Wave Problem in a Generalized Thermo-elastic Solid in the Presence of Voids

B Venkateswara Rao; K Somaiah; A Ravi Kumar; K Narasimharao

doi:10.17485/IJST/v16i19.196

Article

Plane Wave Problem in a Generalized Thermo-elastic Solid in the Presence of Voids

VIEWS 648
PDF 160

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v16i19.196

Year: 2023, Volume: 16, Issue: 19, Pages: 1422-1430

Original Article

Plane Wave Problem in a Generalized Thermo-elastic Solid in the Presence of Voids

B Venkateswara Rao^1*, K Somaiah², A Ravi Kumar³, K Narasimharao⁴

¹Department of Mathematics, SR & BGNR Government Arts & Science College (A), Khammam, 507003, Telangana
²Department of Mathematics, Kakatiya University, Warangal, 506009, Telangana, India
³Department of Mathematics, Satavahana University, Karimnagar, 505002, Telangana, India
⁴Department of Mathematics, Government Degree College for Women, Khammam, 507003, Telangana

*Corresponding Author
Email: [email protected]

Received Date:27 January 2023, Accepted Date:11 April 2023, Published Date:12 May 2023

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

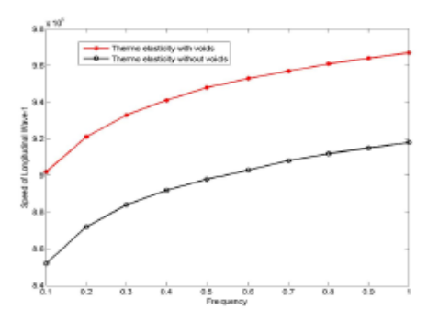
Objective: To investigate the effect of voids on the propagation of plane waves in a generalized thermo-elastic solid. Method: The method of plane harmonic solution is employed to solve the basic equations of generalized thermo-elastic void solids. Findings: Under the effect of voids and non-voids, three sets of longitudinal waves are derived, and they are not appeared in any classical theory of elasticity. But one transverse wave is derived and these results are coinciding with the theory of classical elasticity. Novelty: Under the MATLAB programme the speed of longitudinal waves are shown in the frequency relation. Longitudinal waves are propagating with high speed in nonthermal voids solids.

Keywords: Thermoelasticity; Voids; Plane Harmonic Solution; Plane Longitudinal Waves; Plane Transverse Waves

References

Taylor AG, Chung JH. Elastic Solutions to 2D Plane Strain Problems: Nonlinear Contact and Settlement Analysis for Shallow Foundations. Available from: https://doi.org/10.3390/geotechnics2030032
Cicco SD, Angelis FD. A plane strain problem in the theory of elastic materials with voids. Mathematics and Mechanics of Solids. 2020;25(1):46–59. Available from: https://doi.org/10.1177/1081286519867109
Singh D, Garg M, Tomar. Plane waves in microstretch elastic solid with voids. 2022. Available from: https://doi.org/10.1177/10812865221119826
Iesan D. A theory of thermoelastic materials with voids. Acta Mechanica. 1986;60(1-2):67–89. Available from: https://doi.org/10.1007/BF01302942
Marin M, Öchsner A, Vlase S. Effect of voids in a heat-flux dependent theory for thermo elastic bodies with dipolar structure. Carpathian Journal of Mathematics. 2020;36(3):463–474. Available from: https://www.jstor.org/stable/26932588
Singh SS, Tochhawng L. Stoneley and Rayleigh waves in thermoelastic materials with voids. Journal of Vibration and Control. 2019;25(14):2053–2062. Available from: https://doi.org/10.1177/1077546319847850
Ciarletta M, Scarpetta E. Some Results on Thermoelasticity for Dielectric Materials with Voids. ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik. 1995;75(9):707–714. Available from: https://doi.org/10.1002/zamm.19950750912
Tomar SK, Goyal N, Szekeres A. Plane Waves in Thermo-Viscoelastic Material with Voids Under Different Theories of Thermoelasticity. International Journal of Applied Mechanics and Engineering. 2019;24(3):691–708. Available from: https://doi.org/10.2478/ijame-2019-0043
Kumar A, Tomar SK. Coupled dilatational waves at a plane interface between two dissimilar magneto-elastic half-spaces containing voids. Acta Mechanica. 2022;233(12):5061–5087. Available from: https://doi.org/10.1007/s00707-022-03353-w
Zscheyge M, Böhm R, Hornig A, Gerritzen J, Gude M. Rate dependent non-linear mechanical behaviour of continuous fibre-reinforced thermoplastic composites – Experimental characterisation and viscoelastic-plastic damage modelling. Materials & Design. 2020;193:108827. Available from: https://doi.org/10.1016/j.matdes.2020.108827
Tomar SK, Kumar S. Wave propagation in elastic–plastic material with voids. Journal of Applied Physics. 2020;127(5):054901. Available from: https://doi.org/10.1063/1.5127903
Ciarletta M, Stranghan B, Zampoli V. Thermo Poroacoustic Acceleration Waves in Elastic Materials with Voids without Energy dissipation”. International Journal of Engineering Science. 2007;45(9):736–743. Available from: https://doi.org/10.1016/j.ijengsci.2007.05.001
Chandrasekharaiah DS. Effects of Surface stresses and Voids on Rayleigh waves in an elastic solid. International Journal of Engineering Science. 1987;25:90006–90007. Available from: https://doi.org/10.1016/0020-7225(87)90006-1
Tomar SK, A. Propagating waves in Elastic Materials with Voids Subjected Electro-magnetic interaction. Applied Mathematical Modelling. 2020;78:685–705. Available from: https://doi.org/10.1016/j.apm.2019.10.029
Aoudai M. A theory of thermoelastic diffusion materials with voids. Zeitschrift für angewandte Mathematik und Physik. 2010;61(2):357–379.
Somaiah K, Kumar AR. Investigation of plane longitudinal waves in a micro-isotropic, micro-elastic solid. Journal of Mathematical and Computational Science. 2021;11(1):380–391. Available from: https://doi.org/10.28919/jmcs/5124
Lord HW, Shulman Y. A generalized dynamical theory of thermoelasticity. Journal of the Mechanics and Physics of Solids. 1967;15(5):299–309. Available from: https://doi.org/10.1016/0022-5096(67)90024-5
Achenbach JD, Thau SA. Wave Propagation in Elastic Solids. Journal of Applied Mechanics. 1974;41(2):544.
Dhaliwal RS, Singh. Dynamic Coupled Thermo elasticity. (pp. 726) New Delhi, India. Hindustan Publishing Corporation. 1980.

Copyright

© 2023 Rao et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)