Indian Journal of Science and Technology

Abstract

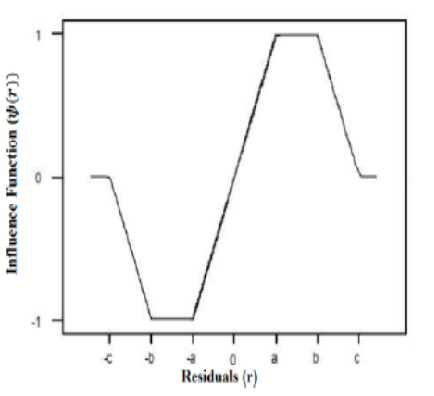
Objectives: To improve the robustness of Support Vector Regression (SVR), Robust Weighted Support Vector Regression (RWSVR) procedure has been proposed by using Hampel’s weight function. It overcomes the drawback by adding weight to each sample observations. Methods: Regression analysis plays a vital role in many areas of science. In this article, the classical regression method, robust regression methods, Support Vector Regression and proposed Robust Weighted Support Vector Regression method are presented. A type of Support Vector Machine (SVM) known as Support Vector Regression (SVR) supports both linear and non-linear regression. This work mainly focuses on Support Vector Regression method. The datasets which are used for this study is StarsCYG, Carbonation and Prostate. Simulation study of three cases are considered with sample size 50,100 and 500 with the contamination levels of 0%, 5%, 10% and 20%. Findings: The most commonly used classical procedure is Least Squares, which is less efficient and very sensitive when the data contains outliers. This work mainly focuses on increasing the accuracy of Proposed method. It overcomes the drawback by adding weight to each sample observations. The efficiency of the proposed method has been observed with the existing regression methods such as Least Squares (LS), Robust Linear Model (RLM) and Support Vector Regression (SVR) by computing various error measures such as Mean Absolute Error (MAE), Median Absolute Error (MDAE), Mean Absolute Percent Error (MAPE) and Root Mean Square Error (RMSE). The proposed RWSVR method is used for the researchers whenever the data contains outliers. Novelty: For getting more accuracy over the conventional SVR, robust Hampel’s weight function is proposed. Newly developed function has a higher mapping power than the commonly used SVR function. The experimental results were carried out on real datasets and simulation study. It shows that the proposed RWSVR is significantly more robust than other regression methods.

Keywords: Least Squares; Robust Regression; Supervised Learning; Support Vector Regression; Hampel’s Weight Function