Solving Fuzzy Fractional Biological Population Model using Shehu Adomian Decomposition Method

S Luvis Savla; R Gethsi Sharmila

doi:10.17485/IJST/v16iSP3.icrtam151

Article

Solving Fuzzy Fractional Biological Population Model using Shehu Adomian Decomposition Method

VIEWS 309
PDF 74

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v16iSP3.icrtam151

Year: 2023, Volume: 16, Issue: Special Issue 3, Pages: 44-54

Original Article

Solving Fuzzy Fractional Biological Population Model using Shehu Adomian Decomposition Method

S Luvis Savla¹, R Gethsi Sharmila^2*

¹Research Scholar, PG & Research Department of Mathematics, Bishop Heber College, (Affiliated to Bharathidasan University), Tiruchirappalli-17, Tamil Nadu, India
²Associate Professor, PG & Research Department of Mathematics, Bishop Heber College, (Affiliated to Bharathidasan University), Tiruchirappalli-17, Tamil Nadu, India

*Corresponding Author
Email: [email protected]

Received Date:05 February 2023, Accepted Date:11 August 2023, Published Date:04 December 2023

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

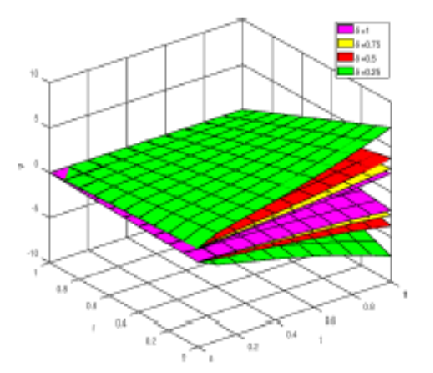
Objectives: In applied sciences and engineering, fuzzy fractional differential equations (FFDEs) are a crucial topic. The main objective of this study is to find the exact solution of the nonlinear Fuzzy Fractional Biological Population Model (FFBPM). In the Caputo concept, fractional derivatives are regarded. Methods: For nonlinear problems, the Shehu transform is difficult to exist. So, the Shehu transform is combined with the Adomian decomposition method is called the Shehu Adomian Decomposition Method (SHADM) and has been proposed to solve the FFBPM. Findings: The main favor of this method is rapidly converging to the exact solution for nonlinear FFDEs. The theoretical proof of convergence for the SHADM and the uniqueness of the solution is given. Novelty: Adomian polynomials are used for nonlinear terms. Figures and numerical examples demonstrate the expertise of the suggested approach. This method is applied for both linear and nonlinear ordinary and partial FFDEs. The proposed approach is rapid, exact, and simple to apply and produce excellent outcomes.

Keywords: Caputo fractional derivative, Shehu transform, triangular fuzzy number, Fuzzy Fractional Biological Population Model, Shehu Adomian decomposition method

References

Benhamed M, Alshehri A, Naeem M, Shah R. Fractional analysis of biological population model via novel transform. Authorea. 2022;p. 1–16. Available from: https://doi.org/10.22541/au.166608723.37031521/v1
Usman M, Khan HU, Khan ZA, Alrabaiah H. Study of nonlinear generalized Fisher equation under fractional fuzzy concept. AIMS Mathematics. 2023;8(7):16479–16493. Available from: https://doi.org/10.3934/math.2023842
Al-Qurashi M, Rashid S, Jarad F, Tahir M, Alsharif AM. New computations for the two-mode version of the fractional Zakharov-Kuznetsov model in plasma fluid by means of the Shehu decomposition method. AIMS Mathematics. 2022;7(2):2044–2060. Available from: https://doi.org/10.3934/math.2022117
Mahdi SH, Jassim HK, Hassan NJ. A new analytical method for solving nonlinear biological population model. In: PROCEEDING OF THE 1ST INTERNATIONAL CONFERENCE ON ADVANCED RESEARCH IN PURE AND APPLIED SCIENCE (ICARPAS2021): Third Annual Conference of Al-Muthanna University/College of Science, AIP Conference Proceedings. Al-Samawah, Iraq, 24–25 March 2021. 2398.
Rashid S, Kubra KT, Guirao JLG. Construction of an Approximate Analytical Solution for Multi-Dimensional Fractional Zakharov–Kuznetsov Equation via Aboodh Adomian Decomposition Method. Symmetry. 2021;13(8):1–22. Available from: https://doi.org/10.3390/sym13081542
Khater MMA. Nonlinear biological population model; computational and numerical investigations. Chaos, Solitons & Fractals. 2022;162. Available from: https://doi.org/10.1016/j.chaos.2022.112388
Sharmila RG, Savla SL. Shehu Transform Method for Linear Fuzzy Fractional Differential Equations. Compliance Engineering Journal. 2021;12(1):257–267. Available from: https://drive.google.com/file/d/1TVV-q_Hcm6PENTLp_k6vQFwYuFYXWF03/view
Shah K, Seadawy AR, Arfan M. Evaluation of one dimensional fuzzy fractional partial differential equations. Alexandria Engineering Journal. 2020;59(5):3347–3353. Available from: https://doi.org/10.1016/j.aej.2020.05.003
Askari S, Allahviranloo T, Abbasbandy S. Solving Fuzzy Fractional Differential Equations by Adomian Decomposition Method used In Optimal Control Theory. International Transaction Journal of Engineering, Management, & Applied Sciences & Technologies. 2019;10(12):1–11. Available from: https://tuengr.com/V10A/10A12P.pdf
Khalouta A, Kadem A. A new method to solve fractional differential equations: Inverse fractional Shehu Transform Method. International Journal of Applications and Applied Mathematics. 2019;14(2):926–941. Available from: https://www.pvamu.edu/aam/wp-content/uploads/sites/182/2019/12/19-R1285_AAM_Khalouta_AK_033019_Published_121119.pdf
Maitama S, Zhao W. New integral transform a generalization of Sumudu and Laplace transform for solving differential equations. International Journal of Analysis and Applications. 2019;17(2):167–190. Available from: https://etamaths.com/index.php/ijaa/article/view/1771
Lydia SK. Solving a system of nonlinear fractional differential equations using mahgoub adomian decomposition method. Bulletin of Pure & Applied Sciences- Mathematics and Statistics. 2019;38E(1):396–404. Available from: https://bpasjournals.com/admin/upload/dynamic2/43jun19.pdf

Copyright

© 2023 Savla & Sharmila. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)