Solving Time-fractional Order Radon Diffusion Equation in Water by Finite Difference Method

Vijaymala Ghuge; T L Holambe; Bhausaheb Sontakke; Gajanan Shrimangale

doi:10.17485/IJST/v17i19.868

Article

$Solving Time-fractional Order Radon Diffusion Equation in Water by Finite Difference Method$

VIEWS 208
PDF 69

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v17i19.868

Year: 2024, Volume: 17, Issue: 19, Pages: 1994-2001

Original Article

Solving Time-fractional Order Radon Diffusion Equation in Water by Finite Difference Method

Vijaymala Ghuge^1*, T L Holambe², Bhausaheb Sontakke³, Gajanan Shrimangale⁴

¹Department of Mathematics, Rashtramata Indira Gandhi College, Jalna, Maharashtra, India
²Department of Mathematics, Late Shankarrao Gutte Gramin Arts, Science and Commerce, Dharmapuri, Beed, Maharashtra, India
³Department of Mathematics, Prathishthan Mahavidyalaya, Paithan, Aurangabad, Maharashtra, India
⁴Department of Mathematics, Mrs. Kesharbai Sonajirao Kshirsagar Alias kaku Arts, Science and Commerce College, Beed, Maharashtra, India

*Corresponding Author
Email: [email protected]

Received Date:21 March 2024, Accepted Date:21 April 2024, Published Date:09 May 2024

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

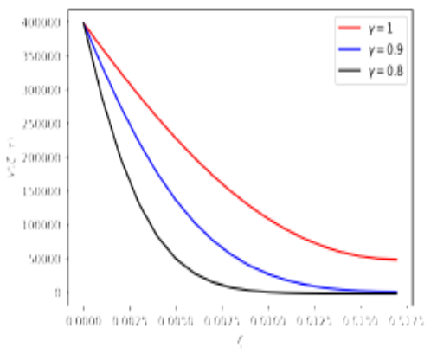
Objective: The aim of this research is to gain a comprehensive understanding of radon diffusion equation in water. Methods: A time fractional radon diffusion equation with Caputo sense is employed to find diffusion dynamics of radon in water medium. The fractional order explicit finite difference technique is used to find its numerical solution. A Python software is used to find numerical solution. Findings: The effect of fractional-order parameters on the distribution and concentration profiles of radon in water has been investigated. Furthermore, we study stability and convergence of the explicit finite difference method. Novelty: The fractional order explicit finite difference method can be used to estimate approximate solution of such fractional order differential equations.

Keywords: Radon Diffusion Equation, Finite Difference Method, Caputo, Fractional Derivative, Python

References

Kumar D, Baleanu D. Editorial: Fractional Calculus and Its Applications in Physics. Frontiers in Physics. 2019;7:1–2. Available from: https://dx.doi.org/10.3389/fphy.2019.00081
Singh J, Hristov JY, Hammouch Z., eds. New Trends in Fractional Differential Equations with Real-World Applications in Physics. (pp. 1-172) Frontiers in Physics. 2009.
Owolabi KM, Atangana A. Numerical Methods for Fractional Differentiation, Springer Series in Computational Mathematics (1). (Vol. 54, p. XVI, 328) Singapore. Springer . 2019.
Kharde U, Takale K, Gaikwad S. Numerical solution of time fractional drug concentration equation in central nervous system. Journal of Mathematical and Computational Science. 2021;11(6):7317–7353. Available from: https://scik.org/index.php/jmcs/article/view/6470
Takale K, Kharde U, Takale G. Fractional Order Mathematical Model to Investigate Topical Drug Diffusion in Human Skin. Indian Journal Of Science And Technology. 2023;16(48):4657–4666. Available from: https://dx.doi.org/10.17485/ijst/v16i48.2113
Kharde U, Takale KC, Gaikwad S. Crank-Nicolson Method for Time Fractional Drug Concentration Equation in Central Nervous System. Adv Appl Math Sci. 2022;22(2):407–433. Available from: https://www.mililink.com/upload/article/1115784474aams_vol_222_december_2022_a4_p407-433_uttam_kharde,_kalyanrao_takale_and_shrikrishna_gaikwad.pdf
Takale K, Kharde U, Gaikwad S. Investigation of Fractional Order Tumor Cell Concentration Equation Using Finite Difference Method. Baghdad Science Journal. 2024;21(9):1–10. Available from: https://dx.doi.org/10.21123/bsj.2024.9246
Shrimangale GW, Raut SR. Crank-Nicolson approximation of fractional order for time fractional radon diffusion equation in soil medium. Journal of Mathematical and Computational Science. 2022;12:1–15. Available from: https://scik.org/index.php/jmcs/article/view/7342
Rao TD, Chakraverty S. Forward and inverse techniques for fuzzy fractional systems applied to radon transport in soil chambers. Chaos, Solitons & Fractals. 2021;147. Available from: https://dx.doi.org/10.1016/j.chaos.2021.110916
Rybalkin A. Numerical and analytical assessment of radon diffusion in various media and potential of charcoal as radon detector. University of Utah thesis
Wang Y, Cai M. Finite Difference Schemes for Time-Space Fractional Diffusion Equations in One- and Two-Dimensions. Communications on Applied Mathematics and Computation. 2023;5(4):1674–1696. Available from: https://dx.doi.org/10.1007/s42967-022-00244-8
Lathkar SV, Ingle RN. Fractional order explicit approximation for time fractional radon diffusion equation and analytical estimates of radon diffusion in air. Malaya Journal of Matematik. 2021;S(1):490–496. Available from: https://doi.org/10.26637/MJMS2101/0113
Yadav S, Kumar D, Nisar KS. A reliable numerical method for solving fractional reaction-diffusion equations. Journal of King Saud University - Science. 2021;33(2):1–8. Available from: https://dx.doi.org/10.1016/j.jksus.2020.101320

Copyright

© 2024 Ghuge et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)