FPGA Implementation of a Novel Two-internal-State Memristor and its Two Component Chaotic Circuit

Njimboh Henry Alombah; Achille Ecladore Tchahou Tchendjeu; Kengne Romanic; Fran ccedil ois Calvin Talla; Hillaire Bertrand Fotsin

doi:10.17485/IJST/v14i27.532

Article

FPGA Implementation of a Novel Two-internal-State Memristor and its Two Component Chaotic Circuit

VIEWS 1395
PDF 255

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v14i27.532

Year: 2021, Volume: 14, Issue: 27, Pages: 2257-2271

Original Article

FPGA Implementation of a Novel Two-internal-State Memristor and its Two Component Chaotic Circuit

Njimboh Henry Alombah^1*, Achille Ecladore Tchahou Tchendjeu², Kengne Romanic³, François Calvin Talla³, Hillaire Bertrand Fotsin³

¹Department of Electrical and Electronics Engineering, College of Technology, University of Bamenda, P.O. Box 39, Bambili, Cameroon
²Department of Computer Engineering, National Higher Polytechnic Institute, University of
Bamenda, P.O. Box 39, Bambili, Cameroon
³Unit of Condensed Matter Research, Electronics and Signal Processing, LAMACET, Faculty of
Science, Department of Physics, University of Dschang, P.O. Box 67, Dschang, Cameroon

*Corresponding Author
Email: [email protected]

Received Date:01 April 2021, Accepted Date:14 July 2021, Published Date:04 August 2021

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

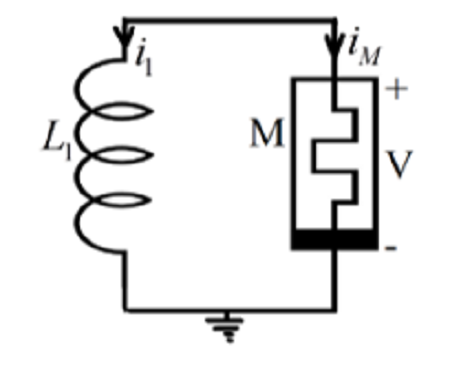
Objectives: To propose a second-order locally- active memristor, a twocomponent chaotic circuit resulting from this current-controlled generic memristor and an application in steganography. Methods/statistical analysis: Using a one-state-variable first-order memristor, a model is proposed which is obtained by modifying a locally-active memristor based on a current-controlled generic memristor. The model has two internal state variables: a voltage stored up in a capacitor and a current stored up in an inductor. With an external inductor, 3D-two-component chaotic circuit is developed. Numerical studies are made using MATLAB and confirmed by a field programmable gate array (FPGA) based hardware implementation. Findings: A two-state-variable based second-order memristor model is presented. The novel memristor configuration leads to the design of a simple two-component chaotic circuit. By investigating the characteristics of the memristor, it is shown that the memristor can be switched from a predominantly passive region to an active region with a wide locally-active region. An application in steganography helps to hide a secrete message inside an image. Application/improvements: The results obtained in this investigation will enrich the literature of memristive circuits, enhance the simplification of chaotic circuits and can be used to improve the memristive circuit based applications in many research domains such as secure information in telecommunications, Random Number Generation (RNG) and image encryption.

Keywords: Memristor; Two component circuit; Chaos; Local activity; FPGA; Steganography

References

Ying J, Wang G, Dong Y, Yu S. Switching Characteristics of a Locally-Active Memristor with Binary Memories. International Journal of Bifurcation and Chaos. 2019;29(11). Available from: 10.1142/S0218127419300301
Wang S, Wang X, Zhou Y, Han B. A memristor-based hyperchaotic complex Lü system and its adaptive complex generalized synchronization. Entropy. 2016;18(2):58. Available from: 10.3390/e18020058
Luo J, Xu X, Ding Y, Yuan Y, Yang B, Sun K, et al. Application of a memristor-based oscillator to weak signal detection. The European Physical Journal Plus. 2018;133(6). Available from: 10.1140/epjp/i2018-12041-y
Alharbi AG, Fouda ME, Khalifa ZJ, Chowdhury MH. Electrical Nonlinearity Emulation Technique for Current-Controlled Memristive Devices. IEEE Access. 2017;5:5399–5409. Available from: https://dx.doi.org/10.1109/access.2017.2695402
Zhao Q, Wang C, Zhang X. A universal emulator for memristor, memcapacitor, and meminductor and its chaotic circuit. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2019;29(013141 ). Available from: 10.1063/1.5081076
Tolba MF, Fouda ME, Hezayyin HG, Madian AH, Radwan AG. Memristor FPGA IP Core Implementation for Analog and Digital Applications. IEEE Transactions on Circuits and Systems II: Express Briefs. 2019;66(8):1381–1385. Available from: https://dx.doi.org/10.1109/tcsii.2018.2882496
Muthuswamy B, Chua LO. Simplest Chaotic Circuit. International Journal of Bifurcation and Chaos. 2010;20(05):1567–1580. Available from: https://dx.doi.org/10.1142/s0218127410027076
Tchitnga R, Fotsin HB, Nana B, Fotso PHL, Woafo P. Hartley’s oscillator: The simplest chaotic two-component circuit. Chaos, Solitons & Fractals. 2012;45(3):306–313. Available from: https://dx.doi.org/10.1016/j.chaos.2011.12.017
Xu B, Wang G, Shen Y. A simple meminductor-based chaotic system with complicated dynamics. Nonlinear Dynamics. 2017;88(3):2071–2089. Available from: 10.1007/s11071-017-3363-y
Talla FC, Tchitnga R, Kengne R, Nana B, Fomethe A. Didactic model of a simple driven microwave resonant T-L circuit for chaos, multistability and antimonotonicity. Heliyon. 2019;5(10):e02715. Available from: https://dx.doi.org/10.1016/j.heliyon.2019.e02715
Deng Y, Li Y. A memristive conservative chaotic circuit consisting of a memristor and a capacitor. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2020;30(1):013120. Available from: 10.1063/1.5128384
Negou AN, Kengne J. Dynamic analysis of a unique jerk system with a smoothly adjustable symmetry and nonlinearity: Reversals of period doubling, offset boosting and coexisting bifurcations. AEU - International Journal of Electronics and Communications. 2018;90:1–19. Available from: https://dx.doi.org/10.1016/j.aeue.2018.04.003
Yuan F, Li Y. A chaotic circuit constructed by a memristor, a memcapacitor and a meminductor. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2019;29(10):101101. Available from: 10.1063/1.5125673
Chua L. Everything You Wish to Know About Memristors but Are Afraid to Ask. In: In Handbook of Memristor Networks. (pp. 89-157) Springer. 2019.
Khalid M. Review on various memristor models, characteristics, potential applications, and future works. Transactions on Electrical and Electronic Materials. 2019;20(4):289–298. Available from: 10.1007/s42341-019-00116-8
Chua LO, Kang SM. Memristive devices and systems. Proceedings of the IEEE. 1976;64(2):209–223. Available from: https://dx.doi.org/10.1109/proc.1976.10092
Sah MP, Yang C, Kim H, Muthuswamy B, Jevtic J, Chua L. A Generic Model of Memristors With Parasitic Components. IEEE Transactions on Circuits and Systems I: Regular Papers. 2015;62(3):891–898. Available from: https://dx.doi.org/10.1109/tcsi.2014.2373674
Adhikari SP, Sah MP, Kim H, Chua LO. Three Fingerprints of Memristor. IEEE Transactions on Circuits and Systems I: Regular Papers. 2013;60(11):3008–3021. Available from: https://dx.doi.org/10.1109/tcsi.2013.2256171
Chua L. If it’s pinched it’sa memristor. Semiconductor Science and Technology. 2014;29(10):104001. Available from: 10.1088/0268-1242/29/10/104001
Ascoli A, Tetzlaff R, Chua LO. The first ever real bistable memristor. IEEE International Symposium on Circuits and Systems (ISCAS). 2016;p. 2896. Available from: 10.1109/ISCAS.2016.7539199
Ascoli A, Slesazeck S, Mahne H, Tetzlaff R, Mikolajick T. Nonlinear Dynamics of a Locally-Active Memristor. IEEE Transactions on Circuits and Systems I: Regular Papers. 2015;62(4):1165–1174. Available from: https://dx.doi.org/10.1109/tcsi.2015.2413152
Wolf A, Swift JB, Swinney HL, Vastano JA. Determining Lyapunov exponents from a time series. Physica D: Nonlinear Phenomena. 1985;16(3):285–317. Available from: https://dx.doi.org/10.1016/0167-2789(85)90011-9
Negou AN, kengne J, Tchiotsop D. Periodicity, chaos and multiple coexisting attractors in a generalized Moore–Spiegel system. Chaos, Solitons & Fractals. 2018;107:275–289. Available from: https://dx.doi.org/10.1016/j.chaos.2018.01.011
Talla FC, Tchitnga R, Fotso PHL, Kengne R, Nana B, Fomethe A. Unexpected Behaviors in a Single Mesh Josephson Junction Based Self-Reproducing Autonomous System. International Journal of Bifurcation and Chaos. 2020;30(07):2050097. Available from: https://dx.doi.org/10.1142/s0218127420500972
Ding Q, Pang J, Fang J, Peng X. Designing of chaotic system output sequence circuit based on FPGA and its applications in network encryption card. International Journal of Innovative Computing, Information and Control. 2007;3(2):449–456.
Sadoudi S, Azzaz MS, Djeddou M, Benssalah M. An FPGA real-time implementation of the Chen’s chaotic system for securing chaotic communications. International Journal of Nonlinear Science. 2009;7(4):467–474.
Rajagopal K, Guessas L, Karthikeyan A, Srinivasan A, Adam G. Fractional Order Memristor No Equilibrium Chaotic System with Its Adaptive Sliding Mode Synchronization and Genetically Optimized Fractional Order PID Synchronization. Complexity. 2017;2017:1–19. Available from: https://dx.doi.org/10.1155/2017/1892618
Wu MY, Ho YK, Lee JH. An iterative method of palette-based image steganography. Pattern Recognition Letters. 2004;25(3):301–310. Available from: 10.1016/j.patrec.2003.10.013
Shehab G, Jawar ZM, Khami M. Matlab Coding For Text Steganography System By Using LSB Insertion Method With Key. Basrah journal of science. 2015;33(2):37–51. Available from: https://iraqjournals.com/article_105863_4adf62c29da0c6082e9e167ada785ad5.pdf
Cheddad A, Condell J, Curran K, Kevitt PM. Digital image steganography: Survey and analysis of current methods. Signal Processing. 2010;90:727–752. Available from: https://dx.doi.org/10.1016/j.sigpro.2009.08.010
Muthukumar P, Balasubramaniam P, Ratnavelu K. Fast projective synchronization of fractional order chaotic and reverse chaotic systems with its application to an affine cipher using date of birth (DOB) Nonlinear Dynamics. 2015;80(4):1883–1897. Available from: https://dx.doi.org/10.1007/s11071-014-1583-y

Copyright

© 2021 Alombah et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)