Fractional Order Mathematical Model to Investigate Topical Drug Diffusion in Human Skin

Kalyanrao Takale; Uttam Kharde; Geetanjali Takale

doi:10.17485/IJST/v16i48.2113

Article

Fractional Order Mathematical Model to Investigate Topical Drug Diffusion in Human Skin

VIEWS 270
PDF 56

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v16i48.2113

Year: 2023, Volume: 16, Issue: 48, Pages: 4657-4666

Original Article

Fractional Order Mathematical Model to Investigate Topical Drug Diffusion in Human Skin

Kalyanrao Takale¹, Uttam Kharde^2*, Geetanjali Takale³

¹Department of Mathematics, RNC Arts, JDB Commerce and NSC Science College, Nashik Road, Nashik, 422101, Maharashtra, India
²Department of Mathematics, S.N. Arts, D.J.M. Commerce and B.N.S. Science College, Sangamner, 422605, Maharashtra, India
³CRSBOX, Senior Project Associates - Public Health CSR, Renalysis Consultants Pvt. Ltd, Ahmedabad, Gujrat, India

*Corresponding Author
Email: [email protected]

Received Date:23 September 2023, Accepted Date:22 November 2023, Published Date:28 December 2023

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

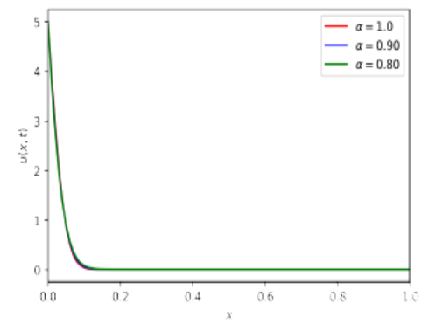
Objectives: The primary objective of this research paper is to gain a comprehensive understanding of drug diffusion within the human dermal region. Methods: A temporal fractional-order reaction-diffusion equation with Caputo sense is employed to get mathematical insights on the diffusion of drugs in the human dermal region. The explicit finite difference method is employed to numerically solve the modelled problem. A Python-based algorithm is employed to obtain a numerical solution through the finite difference method. Finding: In our research, we focused on examining how fractional-order parameters affect the distribution and concentration profiles of drugs in the dermal region. To convey our findings effectively, we conducted a comprehensive analysis, primarily using graphical representations. These visualizations offer a clear and insightful view of the drug's diffusion rate within the dermal region, taking into account the memory effect associated with the Caputo derivative. In addition to our exploration of fractional-order parameters and drug diffusion profiles, we conducted a comprehensive investigation into the stability and convergence of the explicit finite difference method. Novelty: The fractional order explicit finite difference method can be used to estimate drug concentration in the human skin. An algorithm based on Python provides powerful tool for obtaining numerical solution of fractional order differential equations.

Keywords: Drug Diffusion, Numerical Method, Dermal Region, Caputo Derivative, Python

References

Jeong WY, Kwon M, Choi HE, Kim KS. Recent advances in transdermal drug delivery systems: a review. Biomaterials Research. 2021;25(1):1–15. Available from: https://doi.org/10.1186/s40824-021-00226-6
Caputo M, Cametti C. Diffusion through skin in the light of a fractional derivative approach: progress and challenges. Journal of Pharmacokinetics and Pharmacodynamics. 2021;48(1):3–19. Available from: https://doi.org/10.1007/s10928-020-09715-y
Supe S, Takudage P. Methods for evaluating penetration of drug into the skin: A review. Skin Research and Technology. 2021;27(3):299–308. Available from: https://doi.org/10.1111/srt.12968
Jonsdottir F, Snorradottir BS, Gunnarsson S, Georgsdottir E, Sigurdsson S. Transdermal Drug Delivery: Determining Permeation Parameters Using Tape Stripping and Numerical Modeling. Pharmaceutics. 2022;14(9):1–12. Available from: https://doi.org/10.3390/pharmaceutics14091880
Benslimane A, Fatmi S, Taouzinet L, Hammiche D. Mathematical modeling of transdermal drug delivery using microneedle. Materials Today: Proceedings. 2022;53(Part 1):213–217. Available from: https://doi.org/10.1016/j.matpr.2022.01.028
Mubarak S, Khanday MA, Lone A, Rasool N. An analytical approach to study the drug diffusion through transdermal drug delivery system. Appl Math E - Notes. 2021;21:198–208. Available from: https://www.emis.de/journals/AMEN/2021/AMEN-200831.pdf
Čukić M, Galovic S. Mathematical modeling of anomalous diffusive behavior in transdermal drug-delivery including time-delayed flux concept. Chaos, Solitons & Fractals. 2023;172:1–12. Available from: https://doi.org/10.1016/j.chaos.2023.113584
New Trends in Fractional Differential Equations with Real-World Applications in Physics. In: Singh J, Hristov JY, Hammouch Z., eds. Frontiers in Physics. (pp. 1-172) Frontiers Media SA. 2020.
Diethelm K, Kiryakova V, Luchko Y, Machado JAT, Tarasov VE. Trends, directions for further research, and some open problems of fractional calculus. Nonlinear Dynamics. 2022;107(4):3245–3270. Available from: https://doi.org/10.1007/s11071-021-07158-9
Kumar D, Baleanu D. Editorial: Fractional Calculus and Its Applications in Physics. Frontiers in Physics. 2019;7:1–2. Available from: https://doi.org/10.3389/fphy.2019.00081
Joshi H, Jha BK. On a reaction–diffusion model for calcium dynamics in neurons with Mittag–Leffler memory. The European Physical Journal Plus. 2021;136(6). Available from: https://doi.org/10.1140/epjp/s13360-021-01610-w
Sonawane J, Sontakke B, Takale K. Approximate Solution of Sub diffusion Bio heat Transfer Equation. Baghdad Science Journal. 2023;20((1 Special Issue)):394–399. Available from: https://doi.org/10.21123/bsj.2023.8410
Kharde U, Takale K, Gaikwad S. Numerical solution of time fractional drug concentration equation in central nervous system. Journal of Mathematical and Computational Science. 2021;11(6):7317–7336. Available from: https://scik.org/index.php/jmcs/article/view/6470
Rehman MAU, Ahmad J, Hassan A, Awrejcewicz J, Pawlowski W, Karamti H, et al. The Dynamics of a Fractional-Order Mathematical Model of Cancer Tumor Disease. Symmetry. 2022;14(8):1–28. Available from: https://doi.org/10.3390/sym14081694
Mungkasi S. Modelling And Simulation of Topical Drug Diffusion in The Dermal Layer of Human Body. Journal of Advanced Research in Fluid Mechanics and Thermal Sciences. 2021;86(2):39–49. Available from: https://doi.org/10.37934/arfmts.86.2.3949
Owolabi KM, Atangana A. Numerical Methods for Fractional Differentiation, Springer Series in Computational Mathematics (1). (Vol. 54, p. XVI, 328) Singapore. Springer . 2019.
Kharde U, Takale K, Gaikwad S. Crank-Nicolson Method For Time Fractional Drug Concentration Crank-Nicolson Method For Time Fractional Drug Concentration Equation In Central Nervous System. Advances and Applications in Mathematical Sciences. 2022;22(2):407–433. Available from: https://www.mililink.com/upload/article/1115784474aams_vol_222_december_2022_a4_p407-433_uttam_kharde,_kalyanrao_takale_and_shrikrishna_gaikwad.pdf
Ghode K, Takale K, Gaikwad S, Bondar K. Python: Powerful Tool For Solving Space-Time Fractional Traveling Wave Equation. Advances and Applications in Mathematical Sciences. 2022;22(2):503–526. Available from: https://www.mililink.com/upload/article/1168715543aams_vol_222_december_2022_a10_p503-526_krishna_ghode_et_al..pdf

Copyright

© 2023 Takale et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)