Indian Journal of Science and Technology

Abstract

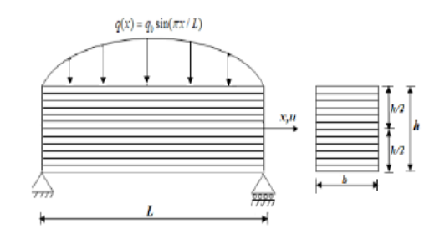
Objectives: This research emphasis on developing solution of transverse displacement for simply supported beam subjected to thermal load using hyperbolic shear deformation theory (HYSDT). Moreover, the significant transverse displacement analysis of single, three-layer orthotropic symmetric laminated beams exposed to sinusoidal thermal loads was taken under consideration with the aim to achieve exact solution for the above condition. Methodology: In this solution, we have used hyperbolic function in reference to thickness co-ordinate by considering shear deformation theory. The governing equations, boundary conditions were developed using principle of virtual work and thus exhibiting solution by Navier’s theory. Findin g: It is observed that by considering single, triple layer transverse displacement for simply supported beam subjected to thermal loading as well as applying hyperbolic shear deformation theory (HYSDT) has predicted transverse displacement of 0.269, 0.210 and 0.562 for ply angles such as 00, 900, 00/900/00 respectively with aspect ratio 20. In accordance with this we observed uniformity among the predicted values. Novelty: In this research we have introduced an advance function such as hyperbolic shear deformation theories (HYSDT) and transverse displacement for variable lengths and thickness of the beam was calculated by using MATLAB coding. Thus, achieving precise solution.

Keywords: Sinusoidal load; hyperbolic shear deformation theory; governing differential equations; MATLAB coding; thermal load