Indian Journal of Science and Technology

Abstract

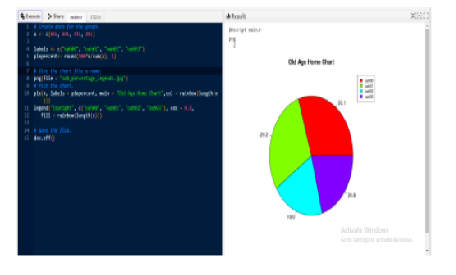
Objectives: A new notion of logical algebra named KM-algebras was introduced in 2019. KM-algebra is a generalization of some of the B-algebras, such as BCK, BCI, BCH, BE, BV-algebras, and d-algebras. Also, by fuzzification of KM-algebras, many exciting results have been analyzed. Now feel obligated to endure dreadful knowledge since no negative interpretation of information is provided. We believe it is also critical to provide mathematical tools to do this. To do this, we develop and utilize a new negative-valued function. Methods: An innovative concept that is Negative valued ideals of KM-algebras has been introduced, and some main results have been proved. The new notion of weak and strong pKM-cut of the Negative valued KM-subalgebras has been introduced. And also, some of the interesting results have been proved. Findings: A very innovative idea of applying Negative valued ideals of KM-algebras, weak and strong pKM-cut of the Negative valued KM-subalgebras in old age homes, and interpreting the outputs in R programming has been analyzed (NKM stands for Negative Valued Function in KM-algebras). Novelty: With the result of this study, on the Negative valued functions of KM-Subalgebras, a very interesting concept of KMM-ideals in Negative valued KM-algebras has been developed. None other than Negative valued ideals of KM-algebras have analyzed more main results using weak and strong pKM-cut of the Negative valued KMsubalgebras. Also, one of the main applications of Negative valued ideals of KM-algebras is, analyzing which Old age Home is better than the other using weak and strong pKM-cut of the Negative valued KM-subalgebras. 2010 AMS Classification: 03G25.

Keywords: KM-algebras, NKM-Structure of Fuzzy KM-algebras, NKM - Subalgebras of Fuzzy KM-algebras, NKM – ideal of KM-algebras, Weak and Strong PKM - cut of NKM - Structure of Fuzzy KM-algebras.