Indian Journal of Science and Technology

Abstract

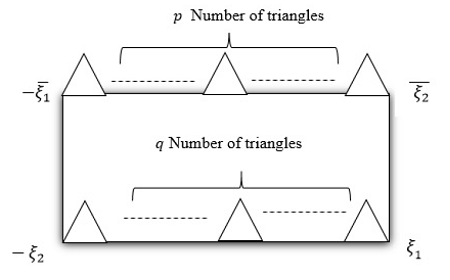
Background/Objectives: Graham Higman gave the idea of coset diagrams for the action of modular group PSL(2;Z) on real quadratic irrationals. These special types of graphical figures are composed of closed paths known as Circuits. These circuits can be classified into certain types of even length with respect to the number of inside\outside triangles. This study is to discuss different properties of reduced numbers in coset diagrams of the type (p;q). Methods: In this study, we have investigated different properties of type (p; q) using reduced quadratic irrationals and continued fractions. We have categorized reduced numbers in accordance with their position in the real line. Distance between two ambiguous numbers and reduced numbers is introduced in this article which will help the reader to understand the structural significance of reduced numbers in a circuit. We have explored different conditions under which certain reduced numbers have the same circuit. Moreover, continued fractions have been used to assist the foundation laid by modular group action and different general results have been derived in this context. Findings: It was possible to define new notions of equivalent, cyclically equivalent and similar circuits using partitions of n and discuss various properties of reduced numbers included in coset diagrams of circuits with length up to four.