Solving Linear and Nonlinear Fuzzy Fractional Volterra-Fredholm Integro Differential Equations Using Shehu Adomian Decomposition Method

S Luvis Savla; R Gethsi Sharmila

doi:10.17485/IJST/v17i12.156

Article

Solving Linear and Nonlinear Fuzzy Fractional Volterra-Fredholm Integro Differential Equations Using Shehu Adomian Decomposition Method

VIEWS 137
PDF 38

Indian Journal of Science and Technology

DOI: 10.17485/IJST/v17i12.156

Year: 2024, Volume: 17, Issue: 12, Pages: 1222-1230

Original Article

Solving Linear and Nonlinear Fuzzy Fractional Volterra-Fredholm Integro Differential Equations Using Shehu Adomian Decomposition Method

S Luvis Savla¹, R Gethsi Sharmila^2*

¹Research Scholar, PG & Research Department of Mathematics, Bishop Heber College (affiliated to Bharathidasan University), Tiruchirapppalli-17, Tamil Nadu, India
²Associate Professor, PG & Research Department of Mathematics, Bishop Heber College (affiliated to Bharathidasan University), Tiruchirapppalli-17, Tamil Nadu, India

*Corresponding Author
Email: [email protected]

Received Date:20 January 2024, Accepted Date:29 January 2024, Published Date:20 March 2024

This work is licensed under a Creative Commons Attribution 4.0 International License.

Abstract

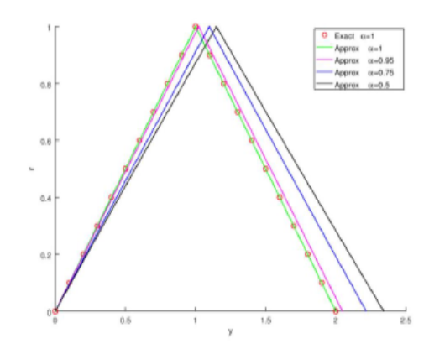
Objectives: In applied sciences and engineering, fuzzy fractional differential equations (FFDEs) and fuzzy fractional integral equations (FFIEs) are a crucial topic. The main objective of this work is to discover an analytical approximate solution for the fuzzy fractional Volterra-Fredholm integro differential equations (FFVFIDE). In the Caputo concept, fractional derivatives are regarded. Methods: The Shehu transform is challenging to exist for nonlinear problems. So, the Shehu transform is combined with the Adomian decomposition method is called the Shehu Adomian decomposition method (SHADM) and has been proposed to solve both linear and nonlinear FFVFIDEs. Findings: Both linear and nonlinear FFVIFIDEs can be solved using this technique. For nonlinear terms, Adomian polynomials have been used. The main benefit of this approach is that it converges quickly to the exact solution. Figures and numerical examples demonstrate the expertise of the suggested approach. Novelty: The comparison between the exact solution and numerical solution is shown in figures for various values of fractional order . The numerical evolution demonstrates the efficiency and reliability of the proposed SHADM. The proposed approach is rapid, exact, and simple to apply and produce excellent outcomes.

Keywords: Fractional calculus, fuzzy number, Mittag Leffler function, Shehu Adomian decomposition method, fuzzy fractional Volterra-Fredholm integro differential equation

References

Thete RB, Jain A. Solution of non-linear integro-differential equations by using modified Laplace transform Adomian decomposition method. Malaya Journal of Matematik. 2021;09(01):1199–1203. Available from: https://www.malayajournal.org/index.php/mjm/article/view/1246
Majid ZA, Rabiei F, Hamid FA, Ismail F. Fuzzy Volterra Integro-Differential Equations Using General Linear Method. Symmetry. 2019;11(3):1–18. Available from: https://doi.org/10.3390/sym11030381
Ullah Z, Ahmad S, Ullah A, Akgül A. On solution of fuzzy Volterra integro-differential equations. Arab Journal of Basic and Applied Sciences. 2021;28(1):330–339. Available from: https://doi.org/10.1080/25765299.2021.1970874
Georgieva A, Spasova M. Solving nonlinear Volterra-Fredholm fuzzy integro-differential equations by using Adomian decomposition method. In: APPLICATIONS OF MATHEMATICS IN ENGINEERING AND ECONOMICS (AMEE’20): Proceedings of the 46th International Conference “Applications of Mathematics in Engineering and Economics”, AIP Conference Proceedings. (Vol. 2333, Issue 1) AIP Publishing. 2021.
Bargamadi E, Torkzadeh L, Nouri K, Jajarmi A. Solving a System of Fractional-Order Volterra-Fredholm Integro-Differential Equations with Weakly Singular Kernels via the Second Chebyshev Wavelets Method. Fractal and Fractional. 2021;5(3):1–14. Available from: https://doi.org/10.3390/fractalfract5030070
Chakraverty S, Tapaswini S, Behera D. Fuzzy Arbitrary Order System: Fuzzy Fractional Differential Equations and Applications. (p. i-xiv, 258) John Wiley & Sons. 2016.
Hasan S, Maayah B, Bushnaq S, Momani S. A modified reproducing Kernel Hilbert space method for solving fuzzy fractional integro-differential equations. Boletim da Sociedade Paranaense de Matemática. 2023;41:1–16. Available from: https://doi.org/10.5269/bspm.52289
Saeed NA, Pachpatte DB, . Usage of the Fuzzy Adomian Decomposition Method for Solving Some Fuzzy Fractional Partial Differential Equations. Advances in Fuzzy Systems. 2024;2024:1–15. Available from: https://doi.org/10.1155/2024/8794634
Alqudah MA, Ashraf R, Rashid S, Singh J, Hammouch Z, Abdeljawad T. Novel Numerical Investigations of Fuzzy Cauchy Reaction–Diffusion Models via Generalized Fuzzy Fractional Derivative Operators. Fractal and Fractional. 2021;5(4):1–40. Available from: https://doi.org/10.3390/fractalfract5040151
Ahmad N, Ullah A, Ullah A, Ahmad S, Shah K, Ahmad I. On analysis of the fuzzy fractional order Volterra-Fredholm integro-differential equation. Alexandria Engineering Journal. 2021;60(1):1827–1838. Available from: https://doi.org/10.1016/j.aej.2020.11.031
Alaroud M, Al-Smadi M, Ahmad RR, Din UKS. An Analytical Numerical Method for Solving Fuzzy Fractional Volterra Integro-Differential Equations. Symmetry. 2019;11(2):1–19. Available from: https://doi.org/10.3390/sym11020205
Rashid S, Jarad F, Abualnaja KM. On fuzzy Volterra-Fredholm integrodifferential equation associated with Hilfer-generalized proportional fractional derivative. AIMS Mathematics. 2021;6(10):10920–10946. Available from: https://doi.org/10.3934/math.2021635
Kumar S, Nieto JJ, Ahmad B. Chebyshev spectral method for solving fuzzy fractional Fredholm–Volterra integro-differential equation. Mathematics and Computers in Simulation. 2022;192:501–513. Available from: https://doi.org/10.1016/j.matcom.2021.09.017
Sharmila RG, Savla L. Shehu Transform Method for Linear Fuzzy Fractional Differential Equations. Compliance Engineering. 2024;12(1):257–267. Available from: https://www.researchgate.net/publication/377964543_Shehu_Transform_Method_for_Linear_Fuzzy_Fractional_Differential_Equations
Savla SL, Sharmila RG. Solving Fuzzy Fractional Biological Population Model using Shehu Adomian Decomposition Method. Indian Journal Of Science And Technology. 2023;16(Special Issue 3):44–54. Available from: https://doi.org/10.17485/IJST/v16iSP3.icrtam151
Maitama S, Zhao W. New Integral Transform: Shehu Transform a Generalization of Sumudu and Laplace Transform for Solving Differential Equations. International Journal of Analysis and Applications. 2019;17(2):167–190. Available from: https://doi.org/10.28924/2291-8639-17-2019-167
Lydia SK. Numerical solution of Volterra integro differential equations of fractional order using Mahgoub Adomian decomposition method. International Journal of Research in Advent Technology (IJRAT). 2019;(Special Issue) 113–118. Available from: https://ijrat.org/downloads/Conference_Proceedings/ICAMBC-19/paper%20ID-25.pdf

Copyright

© 2024 Savla & Sharmila. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Published By Indian Society for Education and Environment (iSee)