Indian Journal of Science and Technology

Abstract

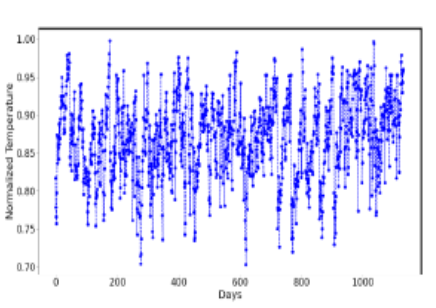
Objective: The aim of this study is to apply different methods to identify chaos in the temperature time series data of Delhi, India, spanning from 1995 to 2019 during the dry season. The goal is to assess the minimum embedding dimension and, consequently, determine the minimum number of factors influencing the temperature time series data. Methods: Lyapunov exponent and correlation dimension calculations have been employed to illustrate the chaotic nature of the data. A plot depicting E2(m) against m has been generated to differentiate data behaviour from stochastic to chaotic. To establish the minimum embedded dimension, an appropriate time lag (τ) has been computed from the plot of Actual Mutual Information (AMI) versus time lag. The Cao method has been utilized to ascertain the minimum embedded dimension. Findings: The Lyapunov exponent value is found to be 0.01900, and the correlation dimension value is 0.90860. The positive Lyapunov exponent value and the non-integral correlation dimension value serve as evidence for the existence of chaos in the data. The minimum AMI value occurs at a time lag of 2 days. Utilizing this minimum AMI value and the Cao method, the minimum embedding dimension is determined to be 7. Therefore, the minimum number of parameters influencing the temperature is identified as 7. Novelty: Unlike many studies that solely rely on the Lyapunov exponent to detect chaos in time series data and use the reconstruction space method to determine embedding dimension, this study incorporates the Cao method for chaotic analysis of time series data. In addition to Lyapunov exponent and correlation dimension, the Cao method is employed to analyse chaotic behaviour and calculate the minimum embedding dimension, providing a comparative analysis between the two methods.

Keywords: Nonlinear dynamics and chaos, Time series data, Lyapunov exponent, Correlation Dimension, State space, Reconstruction space, Embedding space and embedding dimesion